Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 80
Um radiotelescópio está situado na beira de um lago. O telescópio está observando a luz de uma radiogaláxia que está surgindo no horizonte. Se a altura da antena está a 20 m acima da superfície do lago, em que ângulo acima do horizonte a radiogaláxia estará quando o telescópio está centrado no primeiro máximo de intensidade das ondas de rádio? Considere que o comprimento de onda das ondas de rádio é 20 cm. Dica: A interferência é causada pela luz refletida no lago e lembre que esta reflexão resultará em uma mudança de fase de .
Passo 1
Meus lindos e minhas lindas!
As ondas de rádio chegam ao telescópio por 2 caminhos: diretamente da galáxia e pelas ondas refletidas pelo lago. Podemos usar a condição de interferência construtiva das duas ondas para encontrar o ângulo formado em que as ondas possuem essa interferência construtiva.
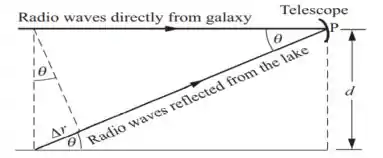
Passo 2
Como o enunciado nos sugere, a reflexão resultará em uma mudança de fase de , logo, no ponto P, a condição de interferência será:
Pelo diagrama, constatamos que:
Porém, quem é
Então:
Aplicando os valores fornecidos pela questão e adotando m = 0:
Transformando de radianos para graus, obtemos que: