Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 84
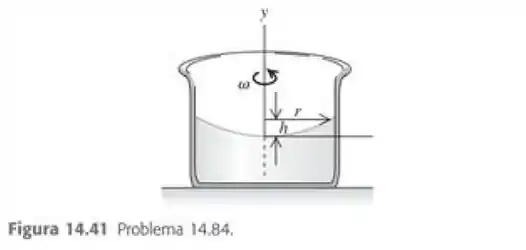
Um recipiente cilindrico contendo um liquido incompressivel de densidade gira com velocidade angular constante em torno de seu eixo de simetria, o qual tomaremos como o eixo (Figura 14.41). a) Mostre que a pressão a uma dada altura no interior do líquido cresce com a distancia radial (para fora do eixo de rotação) de acordo com . b) Integre essa equação diferencial parcial para achar a pressão em função da distancia ao eixo de rotação ao longo de uma linha horizontal para y=0. c) Combine a respsta da paerte (b) com a Equação (14,5) para mostrar que a superficie do liquido que gira possui uma forma parabolica, ou seja, a altura do liquido é dada por . (Essa técnica é usada para fabricar espelhos parabolicos para telescopios ; o vidro liquido gira e depois é solidificado enquanto está girando.)
Passo 1
Aplicando a um pequeno elemento fluido localizado a uma distância do eixo.
Para movimento rotacional:
Passo 2
- A mudança de pressão em relação à distância vertical fornece a força necessária para manter um elemento fluido em equilíbrio vertical (opondo-se ao peso). Para o fluido rotativo, a mudança de pressão com o raio fornece a força necessária para manter um elemento fluido acelerando em direção ao eixo; especificamente,
- Seja a pressão em , a (pressão atmosférica); integrando a expressão para da parte a), temos
E usando
Temos que
Passo 3
Passo 3
Na equação ,
conforme encontrado na parte (b), e , a altura do líquido acima do plano . Usando o resultado da parte (b) obtém-se
A curvatura da superfície aumenta à medida que a velocidade de rotação aumenta.
Resposta
- como mostrado;