Um recipiente contém moléculas de oxigênio a 500 K. (a) Faça um gráfico de precisão da função de distribuição de velocidade de Maxwell em função da velocidade com pontos em intervalos de velocidade de 100 m/s. (b) Determine a velocidade mais provável a partir deste gráfico. (c) Calcule as velocidades média e vmq para as moléculas e coloque esses dados no gráfico. (d) A partir do gráfico, estime a fração de moléculas com velocidades na faixa de 300 m/s a 600 m/s.
Passo 1
Oi tudo bem?
Vamos lá??
- Sabemos que a equação de Maxwell é dada por:
- A velocidade mais provável no gráfico é a maior velocidade possível.
- Para calcular a velocidade média das moléculas, vamos utilizar:
- O número de moléculas pode ser encontrado pela área abaixo da curva.
Na qual a massa do gás é encontrada por:
Passo 2
De acorda com a fórmula anterior, temos o seguintes gráfico:
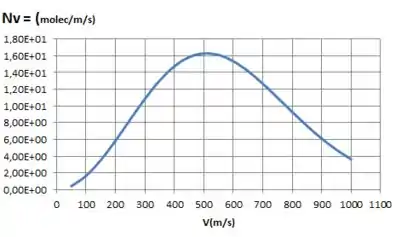
Passo 3
Conforme o gráfico, esta velocidade gira em torno de 500 m/s.
Passo 4
Passo 5
Para calcular a velocidade quadrática média das moléculas, vamos utilizar:
Passo 6
Acrescentando os dados ao gráfico, teremos:
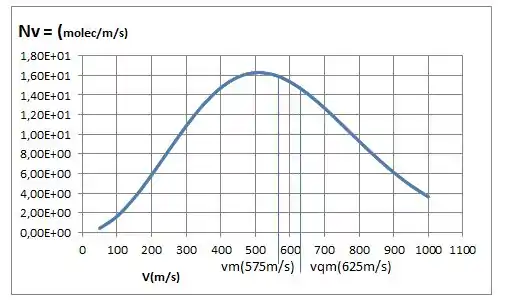
Passo 7
Assim, podemos estimar essa área por:
Resposta
Vide o passo a passo.