Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 9.Problemas - Ex. 3
Um recipiente de paredes adiabáticas é munido de um pistão adiabático móvel, de massa desprezível e de área,, sobre o qual está colocado um peso de . A pressão externa é de . O recipiente contém de gás hélio, para o qual , à temperatura de . (a) Qual é a densidade inicial do gás? Faz-se funcionar um aquecedor elétrico interno ao recipiente, que eleva a temperatura do gás, gradualmente, até . (b) Qual é o volume final ocupado pelo gás? (c) Qual é o trabalho realizado pelo gás? (d) Qual é a variação de energia interna do gás? (e) Quanto calor é fornecido ao gás?
Passo 1
(a) O enunciado já deu o volume do recipiente, então precisamos descobrir a massa para podermos calcular a densidade .
Vamos usar a lei dos gases ideais:
A massa molar do hélio é , o volume do recipiente é , a temperatura é e a constante dos gases é .
E então falta calcular a pressão no interior do recipiente.
Passo 2
Vamos fazer um desenho para ilustrar a situação:
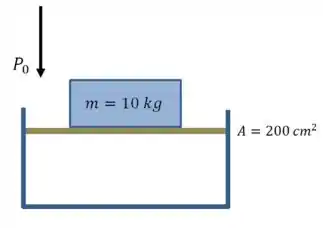
E então a pressão no interior do recipiente é a soma da pressão gerada pelo peso do bloco e a pressão atmosférica:
E então:
E então:
E agora podemos calcular a densidade:
Como é igual a :
Passo 3
(b) Para calcular o volume final ocupado pelo gás, vamos usar a lei dos gases ideais:
O número de moles pode ser calculado usando a massa que calculamos e massa molar do hélio:
E então, como a temperatura sobre até :
Passo 4
(c) Já que o processo ocorre à pressão constante, podemos usar a seguinte fórmula para calcular o trabalho:
Mas agora temos que usar a pressão em Pascal e o volume em metros cúbicos:
Passo 5
(d) O enunciado deu o calor específico à volume constante:
Então podemos calcular a variação de energia interna usando a seguinte fórmula:
E a variação de temperatura é:
Vamos usar a constante dos gases como :
Passo 6
(e) Vamos usar a primeira lei da termodinâmica:
Já calculamos e , então o calor fornecido ao gás é:
Resposta
(a).
(b) .
(c) .
(d) .
(e) .