Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 9.Problemas - Ex. 7
de gás hélio, com , inicialmente nas condições , é submetida aos seguintes processos: (i) Expansão isotérmica até o dobro do volume inicial; (ii) Aquecimento a volume constante, absorvendo ; (iii) Compressão isotérmica, até voltar ao volume inicial. (a) Represente os processos no plano , indicando (em atm), (em ) e em ) associado a cada ponto. (b) Calcule e para os processos (i), (ii) e (iii).
Passo 1
Vamos começar seguindo as instruções do enunciado para desenhar o diagrama do processo:
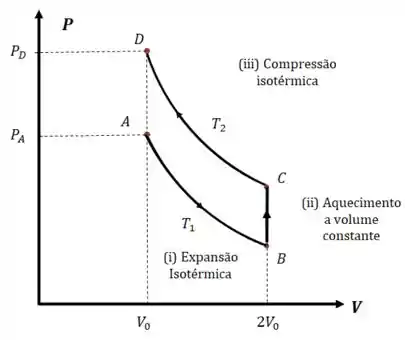
Já que inicialmente estamos nas condições , podemos dizer que:
E como a massa molar do hélio é , uma massa de corresponde a .
Podemos usar isso tudo para calcular :
E o volume , então:
Passo 2
Sabendo que entre o ponto e o ponto o gás absorve e não realiza nenhum trabalho:
Agora é só substituir os valores numéricos:
Aqui nós usamos , já que a variação de energia interna estava em joules.
E essa é a mesma temperatura do ponto , então podemos usar isso para calcular :
Agora vamos completar o gráfico com esses valores:
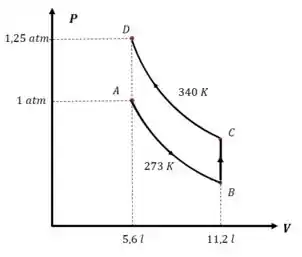
Passo 3
(b) Agora queremos calcular a variação de energia interna e o trabalho realizado pelo gás em cada um dos processos.
Começando pelo processo , que é uma expansão isotérmica.
E podemos usar a fórmula para calcular o trabalho:
No processo , que é um processo isovolumétrico, temos:
E para a energia interna podemos usar a seguinte fórmula:
E finalmente, para o processo , que também é isotérmico, temos:
Resposta
(a) Ver desenho.
(b) e ; e ; e .