Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 38
Um relógio de parede tem um ponteiro de minutos com um comprimento de e um ponteiro de horas com um comprimento de . Tome o centro do relógio como a origem, e usa um sistema de coordenadas cartesiano com o eixo positivo apontando para o e o eixo positivo apontado para o ; Usando os vetores unitários e , expresse os vetores posição das pontas dos ponteiros de horas () e de minutos () quando o relógio indica (a) , (b) , (c) , .
Passo 1
Em um relógio nós temos pelo menos pontos igualmente espaçados em torno de uma circunferência, isso quer dizer que o ângulo entre eles é:
Isso quer dizer que, entre dois números do relógio, nós temos uma separação de . Para seguir as convenções, vamos contar no sentido anti-horário a partir do eixo .
Nesse caso, está sobre o , está sobre o , está sobre o , e assim por diante.
Em termos dos vetores e , as posições das pontas dos ponteiros vão seguir uma fórmula simples:
E como todas os itens pedem horas “redondas”, o ponteiro dos minutos sempre estará sobre o :
Passo 2
Só precisamos descobrir quais são os ângulos associados a cada número, seguindo a nossa lógica de antes fica fácil completar uma tabela:
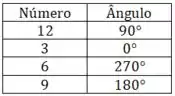
E agora é só usar a nossa fórmula de antes:
(a) Para :
(b) Para :
(c) Para :
(d) Para :
Resposta
(a) . .
(b) . .
(c) . .
(d) .