Resolva a equação de Schrödinger in- ependente do tempo para um poço quadrado infinito com uma barreira função delta no meio:

Considere as funções de onda par e impar separadamente. Não é necessário normalizá-las. Calcule as energias permitidas (graficamente, se necessário), Como elas podem ser comparadas às energias correspondentes na ausência da funçăo delta? Explique por que as soluções impares não são afetadas pela função delta. Comente os

Ok! Já entendemos as equações de onda. Agora, vamos pensar nas condições que o problema nos estabeleceu:

A primeira condição é, que se for contínuo em 0, então B=B!

A segunda, é que se for descontínuo, então a equação a utilizar é:

Por último, temos o caso em que tente a 0 em x=a:

Assim, conseguimos encontrar a equação de onda para quando :

Como temos, para esta equação, a influência da tangente do ângulo, que compõe assíntotas. Ao compor um gráfico, perceberemos que as energias permitidas estarão acima, ou seja:

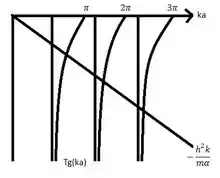
Como podemos ver,

Então, encontramos a energia:

Como podemos perceber, essas energias são mais altas do que as vistas no capítulo, em especial na equação 2.27, do poço quadrado infinito. Como podemos analisar no gráfico, quando α → 0, a seção linear (de equação -2k/mα) fica cada vez mais íngreme, enquanto as intersecções se aproximam de nπ/2, até que as energias se reduzam àquelas da equação 2.27, do infinito comum. Logo, à medida que α → ∞, a linha reta se aproxima da horizontal, é quando as intersecções chegam a nπ e, assim, a energia tende a atingir a equação encontrada, em função da largura a do poço infinito.