Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Griffiths - Mecânica Quântica- Ed: 2º - Capítulo 2.Problemas - Ex. 36

Resolva a equação de Schrödinger independente do tempo com condições de contorno apropriadas para o poço quadrado infinito ‘centrado’: V ( x ) = 0 (para - a < x < + a ) ,   V ( x ) = ∞ (caso contrário). Verifique se as energias permitidas são consistentes com as minhas (equação 2.27) e confirme se suas ψ podem ser obtidas a partir das minhas (Equação 2.28) pela substituição x → ( x + a ) / 2 (além da renormalização apropriada). Esboce as três primeiras soluções e compare-as com a Figura 2.2. Note que, agora, a largura do poço é de 2a.

Passo 1

Vamos começar com a equação 2.22:

ψ ( x ) = A   s i n   k x + B   c o s   k x

Desta vez as condições de limite são ψ ( a ) =   ψ ( - a ) = 0

Sendo assim, temos:

A   s i n   k a + B   c o s   k a = 0     ;       - A   s i n   k a + B   c o s   k a = 0    

Cosseno é uma função par, por isso o sinal de sua parcela não se altera. Essas duas equações nos fornecem um sistema de equações, então, nós podemos obter as relações através da soma delas:

S u b t r a ç ã o ;   A   s i n   k a = 0   ⟹               k a =   j π   o u   A = 0   A d i ç ã o ;   B   s i n   k a = 0   ⟹   k a =   j - 1 2 π   o u   B = 0    

Para j= 1,2,3….

Passo 2

Analise:

  • Se B = 0 A ≠ 0 ,   k = j π / a .

    • Nesse caso temos n ≡ 2 j (sendo n um número inteiro par); então k =   n   π / 2 a , então:

    ψ = A   s i n n π x / 2 a

    Normalizando: 1 =   A 2 ∫ - a a s i n 2 ( n \ p i   x / 2 a ) d x =   A 2 2 = A = 2 .

  • Se A = 0 B ≠ 0 , k = j - 1 2 π / a .

Nesse caso vamos n ≡ ( 2 j - 1 ) (sendo n um número inteiro ímpar); novamente k =   n   π / 2 a , então:

ψ = B c o s n π x / 2 a

Normalizando: 1 =   B 2 ∫ - a a c o s 2 ( n \ p i   x / 2 a ) d x =   B 2 2 = B = 2 .

Em ambos os casos k satisfaz a equação 2.21 e produz:

E = ℏ 2 k 2 2 m =   ℏ 2 π 2 n 2 2 m   ( 2 a ) 2

Que está de acordo com Eq. 2.27 E = ℏ 2 π 2 n 2 2 m   ( a ) 2 , para um poço de largura 2a.

Passo 3

Com a substituição x   →   ( x + a ) / 2 , leva a equação2.28 também:

Ψ n ( x ) = 2 a s i n   n   π a x → 2 a s i n   n   π a x + a 2

Ψ n ( x ) = 2 a s i n   n   π   x 2 a + n   π 2

  Ψ n ( x ) = ( - 1 ) n / 2   2 a s i n   n   π x 2 a ,     ( n   p a r ) ( - 1 ) ( n - 1 ) / 2 2 a c o s   n   π x 2 a ,     ( n   í m p a r )

Passo 4

Os gráficos são os mesmos da Figura 2.2, exceto que alguns estão de cabeça para baixo (normalização diferente).

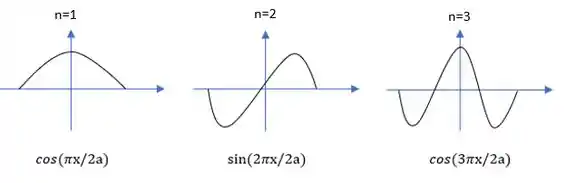
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro