Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 6.Problemas - Ex. 2

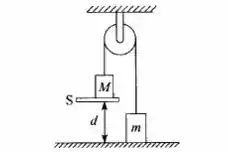
No sistema da figura, M= 3 Kg, m= 1 Kg e d = 2 m. O suporte S é retirado num dado instante. a) Usando conservação de energia, ache com que velocidade M chega ao chão. b) Verifique o resultado, calculando a aceleração do sistema pelas leis de Newton.

Passo 1

  1. Como o problema sugere, vamos utilizar conservação de energia mecânica para resolver essa questão. Chega mais!

    2. Δ E = 0

    Considerando o sistema composto pelas 2 massas, vamos escrever termo a termo as variações de energia cinética e potencial,

    Δ K M + Δ U M + ( Δ K m + Δ U m ) = 0

    Explicitando cada termo,

    M v 2 2 - M g d + m v 2 2 + m g d = 0  

    Sabemos que a velocidade final do bloco maior é a mesma velocidade final do bloco menor, já que estão conecatos pelo cabo e só podem ter a mesma taxa de deslocamento. Pronto, bora lá

    v 2 2 M + m + g d m - M = 0

    Isolando a velocidade,

    v = 2 g d M - m M + m

    =   2   .   9,8   .   2 3 - 1 3 + 1 = 4,43   m / s

    Passo 2

  2. Considerando o sistema de 2 blocos como únicos e que as forças internas de tração se cancelam podemos escrever a lei de Newton assim

( M + m ) a = M - m g

→

a = M - m M + m g

= 4,9   m / s 2

Para saber a velocidade final do bloco vamos utilizar torricelli

v 2 = 2 a d

→

v = 9,8   .   2

= 4,43   m / s

Resposta

v =   4,43   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quanto trabalho é feito pela vizinhança no processo representado na FIGURA EX11.28? A energia é transferida da vizinhança para o sistema ou em sentido contrário?
Um sistema perde 400 J de energia potencial. No processo, ele realiza 400 J de trabalho sobre a vizinhança e a energia térmica aumenta em 100 J. Represente o processo por um gráfico de barras de energ
Um sistema ganha 500 J de energia cinética enquanto perde 2.000 J de energia potencial. A energia térmica aumenta em 100 J. Represente o processo por um gráfico de barras de energia
Um bloco de massa m é derrubado do quarto andar de um prédio de escritórios e atinge a calçada abaixo na velocidadev . A partir de que andar a massa deve ser derrubada para dobrar a velocidade escalar
Por que a seguinte situação é impossível? Em um cassino novo, uma máquina de pinball superdimensionada é apresentada. A publicidade do cassino alardeia que um jogador de basquete profissional pode dei