Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 13.Problemas - Ex. 8

Em que latitude λ o ângulo de desvio entre a direção de um fio de prumo e a direção radial verdadeira (que aponta para o centro da Terra) é máximo? Quanto vale o ângulo de desvio máximo?

Passo 1

Mudando para o referencial do fio, vamos trocar a resultante centrípeta apontando para o centro de rotação por uma força de mesmo módulo apotando para fora, assim ó:

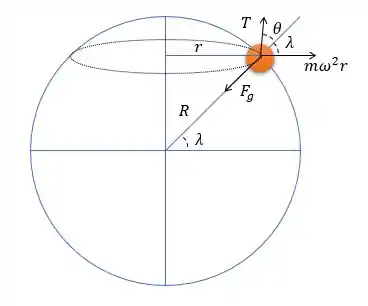
Vamos considerar que nossa amplitude é λ e o desvio entre a direção de um fio de prumo e a direção radial verdadeira é θ . Como nosso sistema está em equilíbrio, temos:

∑ F → = 0

Na direção tangencial:

m ω 2 r s e n λ - T s e n θ = 0 → T = m ω 2 r s e n λ s e n θ

Na direção radial:

m ω 2 r c o s λ + T c o s θ - F g = 0

Passo 2

Da primeira equação já temos o valor de T . Além disso, sabemos que F g = m g . Usando isso na segunda equação, temos:

m ω 2 r c o s λ + m ω 2 r s e n λ s e n θ ⋅ c o s θ - m g = 0

Repara que não sabemos o valor de r , mas da figura conseguimos verificar que r = R c o s ( λ ) . Assim,

m ω 2 ⋅ R c o s λ ⋅ c o s λ + m ω 2 ⋅ R c o s ( λ ) ⋅ s e n λ s e n θ ⋅ c o s θ - m g = 0

Isto é,

m ω 2 ⋅ R c o s 2 λ + m ω 2 R c o s λ s e n λ t g θ - m g = 0

ω 2 R c o s λ s e n λ t g θ = g - ω 2 ⋅ R c o s 2 λ

Logo,

t g θ = ω 2 R c o s λ s e n λ g - ω 2 ⋅ R c o s 2 λ

Passo 3

Para facilitar nossa vida, podemos fazer uma simplificação aqui. A velocidade de rotação da terra é em torno de v = 465   m / s e o raio da terra é R = 6400   k m . Então nosso fator ω 2 ⋅ R c o s 2 λ será:

ω 2 ⋅ R = v 2 R 2 ⋅ R = 465 m s 2 6400 × 10 3   m 2 ⋅ 6400 × 10 3   m 2 ≅ 0,033

Como 0 ≤ cos 2 ⁡ λ ≤ 1 :

0 ≤ ω 2 ⋅ R c o s 2 λ ≤ 0,003

O que é desprezível perto de g = 9,81   N / k g . Assim,

t g θ ≈ ω 2 R c o s λ s e n λ g

Como s e n 2 λ = 2 s e n λ cos ⁡ λ ,

t g θ ≈ ω 2 R 2 g ⋅ s e n ( 2 λ )

Portanto, o ângulo será máximo quando s e n 2 λ = 1 . Logo,

2 λ = π 2 → λ = π 4

Portanto, o ângulo de desvio máximo será:

t g θ ≈ ω 2 R 2 g = 0,033 2 ( 9,81 )

θ = arctan ⁡ 0,033 2 ( 9,81 ) = 0,0017

Resposta

λ = π 4

θ = arctan ⁡ ω 2 R 2 g = 0,0017

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

65. Uma mola leve tem comprimento não distendido de 15,5c m . Ela é descrita pela lei de Hooke com constante elástica de 4,30N / m . Uma extremidade da mola é mantida sobre um eixo vertical fixo e a o
Uma haste rígida isolante, com duas cargas de sinal oposto e módulos diferentes presas às suas extremidades, é colocada em um campo elétrico uniforme E → , como mostrado na figura abaixo. A haste sofr
Na Figura 5.12 vê-se uma pedra de massa m , suspensa por um fio, em uma órbita circular em um plano horizontal. A) Identifique as forças que atuam sobre a pedra. B) Qual é a tensão T no fio? C) Qual é
Como mostra a Figura 5.11, uma pedra gira no ar, presa por um fio de comprimento l . A) Qual é a tensão no fio? (Ignore a gravidade.) B) Se o fio arrebentar quando a pedra estiver na posição mostrada
Uma pedra com massa de 0,80k g está presa à ponta de um fio com 0,90m de extensão. O fio se romperá se a tensão ultrapassar 60,0N . A pedra é girada em um círculo horizontal sobre uma mesa sem atrito;