Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.11 - Ex. 61
Suponha que N elétrons possam ser colocados em duas configurações diferentes. Na configuração 1, todos os elétrons estão distribuídos uniformemente ao longo de um anel circular estreito de raio R. Na configuração 2, N - 1 elétrons estão distribuídos uniformemente ao longo do anel e o elétron restante é colocado no centro do anel.
(a) Qual é o menor valor de N para o qual a segunda configuração possui menor energia que a primeira?
(b) Para esse valor de N considere um dos elétrons do anel, . Quantos outros elétrons do anel estão mais próximos de que o elétron central?
Passo 1
Letra (a)
Primeiro, meu caro ou minha cara, vamos calcular a distância d entre pontos na circunferência separados por um ângulo :
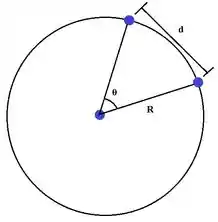
Vamos pegar um triângulo ali dentro para conseguir calcular o d:
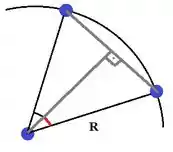
O ângulo vermelho vale . O seno dele é:
Pronto, achamos o d:
Passo 2
Agora você vai ficar irritado comigo, mas não é culpa minha ☹. Você já sabe calcular a distância entre dois pontos na circunferência, né? Então sabe calcular a energia potencial entre eles:
Só que não tem só dois pontos na circunferência. A energia potencial é a soma de todos os pares... sim, tem que usar essa fórmula que a gente achou váaaarias vezes. Quantas vezes, você pergunta? Tantas vezes quantos forem os pares. Se N for 6 teremos pares (lembra de combinatória?). Então é só multiplicar por 15? Não, porque o ângulo muda. Por exemplo, se você pega duas cargas consecutivas, o vale um valor, mas se você pega duas cargas não consecutivas, o que vai na fórmula é outro. Então não tem fuga.
Vou te dar essa tabela com o valor da energia potencial para vários valores de N, para as duas configurações:
O número que aparece na tabela vai multiplicar esse termo:
Ou seja, uma circunferência com 10 elétrons, na configuração 1, tem energia:
Olhando a tabela, a partir de 12 elétrons, a segunda configuração tem menor energia que a primeira. Na minha opinião, é uma questão totalmente desnecessária, mas...
Passo 3
Letra (b)
N = 12, certo? Certo. Vamos olhar para a configuração 2, porque é ela que tem um elétron no centro do disco. Então temos 11 elétrons na periferia do disco. Os elétrons mais próximos de (e que estão na periferia) estão a uma distância:
Estão mais próximos do que o do centro. Agora os próximos:
Logo, estes estão mais longe de do que o elétron do centro. Então gente, só tem 2 elétrons na periferia que estão mais próximos de (um de cada lado) do que o elétron do centro
Resposta
Letra (a): N = 12
Letra (b): 2 elétrons