Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.4 - Ex. 11
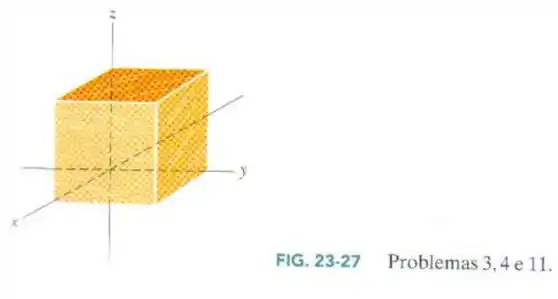
A Fig. 23-27 mostra uma superfície gaussiana com a forma de um cubo com 1,40 m de aresta. Determine (a) o fluxo Φ através da superfície; (b) a carga qenv envolvida pela superfície se E = (3,00y ĵ ) N/C, com y em metros; os valores de (c) Φ e ( d) qenv se E = [ - 4,00 î + (6,00 + 3,00y) ĵ] N/C.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui a atividade é bem direta sobre o que ela quer.
Para determinar o fluxo que passa através da superfície temos que utilizar o campo dado no item (b) e a seguinte definição de fluxo elétrico:
Passo 2
Como o campo só tem componente na direção , só há fluxo nas faces da direita e da esquerda, portanto:
Lembrando que o fluxo que entra dentro da superfície gaussiana é negativo.
Passo 3
Para o item (b), basta utilizar a lei de Gauss:
Passo 4
O item (c) vamos fazer algo parecido com o item (a), porém, como o campo agora tem componentes na direção , vai haver fluxo na face frontal e traseira. Mas podemos simplificar se percebemos que o campo elétrico na face frontal e traseiras é constante, assim o fluxo, somado, dessas faces será zero. Dessa forma, precisamos levar em conta apenas o fluxo da face esquerda e direta:
Passo 5
Como o fluxo através da superfície é o mesmo do item (a), no item (d), a carga vai ser a mesma do item (b):
Resposta
(a)
(b)
(c)
(d)