Suponha que um flautista toque uma nota Dó de 523 Hz com amplitude de deslocamento do primeiro harmônico . A partir da Figura 14.14b, leia, por proporção, as amplitudes de deslocamento dos harmônicos 2 até 7. Considere essas amplitudes como os valores até na análise do som de Fourier e suponha que . Construa um gráfico da forma de onda do som. Sua forma de onda não será exatamente como a de onda da flauta na Figura 14.13b porque você simplifica desprezando os termos cosseno; apesar disso, ela produz a mesma sensação na audição humana.
Passo 1
Falaaa galerinhaaa,
Sabemos que a série de Fourier é apresentada da seguinte forma em sua fórmula geral:
Passo 2
Por construção, com uso de uma régua graduada e cálculo de proporção, podemos estimar os valores dos coeficientes de ; para variando de 1 a 7, os valores são respectivamente : 100; 143; 57; 106; 51; 29; 26.
As frequências mais altas são múltiplos inteiros da frequência fundamental,
Em particular, os valores dos coeficientes são nulos. Com isso, a equação da série de Fourier se simplifica para:
Passo 3
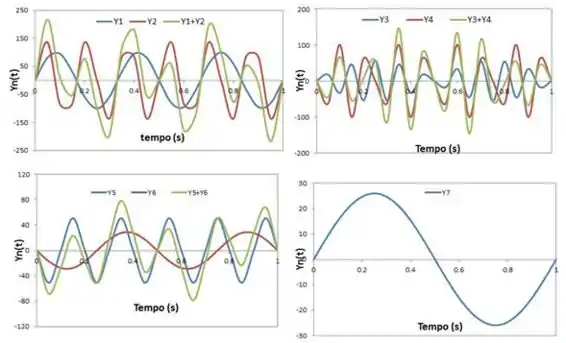
As figuras a seguir mostram os gráficos das funções de onda apresentadas anterior
No primeiro gráfico, temos
No segundo :
No terceiro :
No quarto gráfico temos :
Passo 4
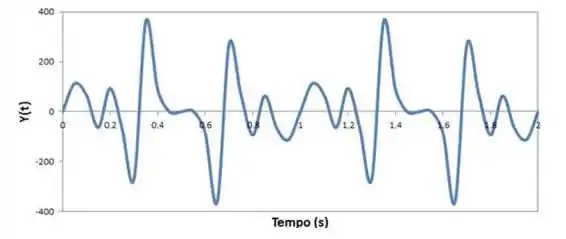
A onda sonora resultante é a soma das três primeiras curvas verdes, nos três primeiros gráficos, com a última curva, . O gráfico mostrando a cursa resultante desta soma é apresentado a seguir:
Resposta
Vide a explicação.