Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 9.Problemas - Ex. 9

Suponha que as partículas do Prob. 9.7 estejam nos pontos (0,1,1) e (-1, O, 2), respec-

tivamente. (a) Determine a posição do CM. (b) Determine o momento angular do sistema relativamente ao seu CM. (c) Obtenha o momento angular relativamente à origem.

Passo 1

Falaaa galera!!!

Aqui, como já utilizamos em 9.7 e em 9.8, temos os seguintes dados:

m 1 = 2 k g ,   m 2 = 3 k g ,   v 1 = 10   m / s ,   v 2 = 8   m / s

Assim, vamos relembrar a fórmula utilizada para encontrar a posição do centro de massa:

Y c m = ∑ m i * v i / m = 2 ( j + h ) + 3 ( - i + 2 h ) / 5 = ( - 0,6 i + 0,4 j + 1,6 h ) m  

Passo 2

Pela definição, temos que:

i c m = r 1 ' p 1 ' + r 2 ' p 2 '

Dos exercícios anteriores, vamos lembrar que

r 1 ' = - 0,6 i + 0,6 j - 0,6 h

v 1 ' = 8,4 i - 2,4 3 j

r 2 ' = - 1,6 i - 0,4 j + 0,4 h

v 2 ' = - 5,6 i + 1,6 3 j

Assim, temos que:

i c m = ( - 0,6 i + 0,6 j - 0,6 h ) * 2 * ( 8,4 i - 2,4 3 j ) + ( - 1,6 i - 0,4 j + 0,4 h ) * 3 * ( - 5,6 i + 1,6 3 j )

Para resolvermos isso, precisamos calcular o determinante da matriz que envolve cada um destes valores, considerando i, j e k, vetores unitários.

Nós teremos que:

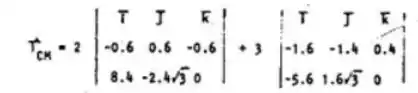
A partir disso, calculando o determinante, teremos:

i c m = ( - 8,3136 i - 16,8 j - 25,1136 k ) k g * m ² / s

Passo 3

Em c, teremos que:

i = r 1 p 1 + r 2 p 2

Utilizando os dados encontrados em 9.7, teremos:

i = - 24 3 i - 4 j - ( 20 + 12 3 ) k = ( - 41,568 i - 4 j - 40,784 k ) k g * m ² / s

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro