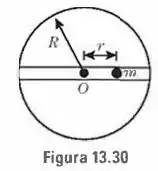
Suponhamos que fosse aberto um canal que atravessasse a Terra completamente, ao longo de um diâmetro (Fig. 13.30). (a) Mostre que a força, sobre uma massa , a uma distância do centro da Terra, será , se admitirmos que a densidade seja uniforme, (b) Mostre que o movimento de m seria harmônico simples, com um período de aproximadamente de . (c) Escreva as equações para a posição velocidade e aceleração como funções do tempo, dando os valores numéricos das constantes.
Passo 1
E aí, beleza?? Da lei de Gauss gravitacional, temos:
Portanto, aplicando a uma superfície esférica de raio :
Portanto, a força é:
Passo 2
Assim, da segunda lei de Newton, vem:
Portanto, fica demonstrado assim que o movimento é um MHS, com período dado por:
Passo 3
Para e , vem:
Com em quilômetros e em horas. Derivando:
Para a aceleração, derivando novamente e convertendo para :