Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 34.Exercícios e Problemas - Ex. 29
Temos uma espira quadrada de e resistência total igual a , e um campo magnético perpendicular à espira com módulo , onde B está em tesla, e t, em segundos.
- Determine B, e I em intervalos de meio segundo, desde 0 s até 2 s.
- Use os resultados do item anterior para desenhar os gráficos de B e de I em função do tempo.
Passo 1
Faaaaaala, galera... Tranquileba??
Sabemos que:
E que:
Sendo o campo paralelo a A:
Assim:
E a corrente é:
Bora pro próximo passo?!
Passo 2
Assim, façamos em intervalos de
Para t=0
Para t=0.5 s:
Para t=1 s
Para t=1.5 s:
Para t=2:
Passo 3
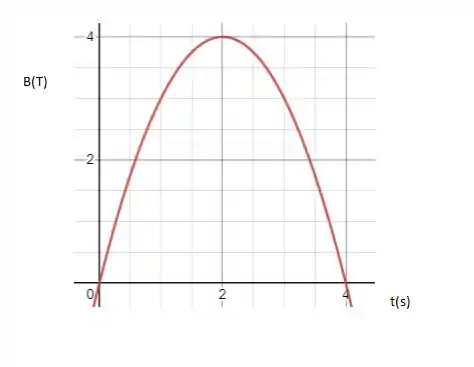
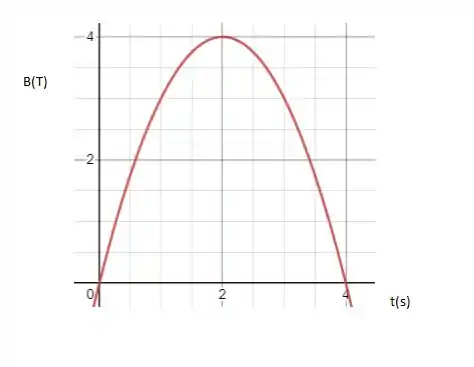
Para B)
Obtemos o gráfico para B(t):
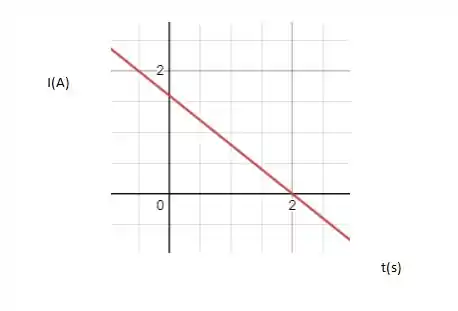
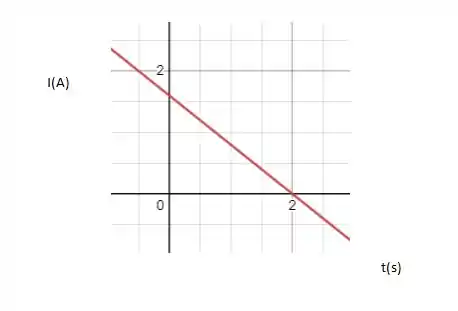
E para a corrente:
Resposta
Para t=0
Para t=0.5 s:
Para t=1 s
Para t=1.5 s:
Para t=2:
Para b)
