Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.5 - Ex. 51a
Um toróide de seção reta quadrada, com de lado e um raio interno de , tem espiras e conduz uma corrente de . (O toroide é feito a partir de um solenóide quadrado, em vez de redondo, como o da figura 29-16) Determine o campo magnético no interior do toróide (a) a uma distância do centro igual ao raio interno.
Passo 1
Fala aí! tudo certinho? 😁
Nesse problema temos um toróide de seção reta quadrada, com de lado e um raio interno de . Ele tem espiras e conduz uma corrente de .
A partir daí queremos determinar o campo magnético no interior do toróide a uma distância do centro igual ao raio interno.
Tem ideia de como fazer isso? 🤔
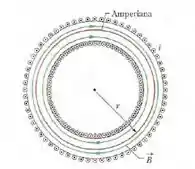
Por simetria, vemos que as linhas de formam circunferências concêntricas no interior do toroide, como mostra a figura abaixo.
Vamos escolher como amperiana uma circunferência de raio e percorrê-la so sentido horário.
De acordo com a lei de Àmpere, temos:
em que é a corrente nas espiras do toroide (que é positiva para as espiras envolvidas pela amperiana) e é o número total de espiras.
Veja só! 😁
Passo 2
Assim, temos:
De acordo com a equação acima, temos:
Sacou a ideia? Responde Aí! 😉
Resposta
O campo magnético é: