Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.Problemas Adicionais - Ex. 88
A torre de pisa tem de altura e de diâmetro. O alto da torre está deslocado em relação à vertical. Modele a torre como um cilindro circular homogêneo. (a) Que deslocamento adicional do alto da torre faria com que a torre ficasse no limiar de tombar? (b) Qual seria o ângulo correspondente da torre em relação à vertical?
Passo 1
(a) Vamos fazer um diagrama que represente a torre quanto ela está prestes a tombar:
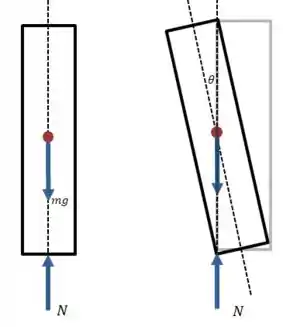
Para tombar, a força peso deve ser capaz de produzir um torque que faça a torre girar em torno do último ponto de contato com o chão.
Ou seja, a torre precisa se inclinar o suficiente para que a linha de ação da força peso não esteja sobre o pé da torre.
Para isso, o pé da torre não precisa de deslocar em relação à vertical, o centro de massa tem que se deslocar por uma distância igual ao raio da base da torre, e o topo precisa de deslocar por uma distância igual ao diâmetro da base da torre.
Isso fica bem claro pelo desenho:
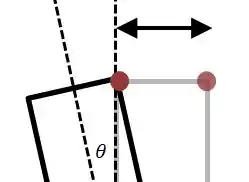
Como a torre já se deslocou por , o deslocamento adicional necessário é:
Passo 2
(b) O ângulo correspondente a essa posição também pode ser calculado a partir do desenho:
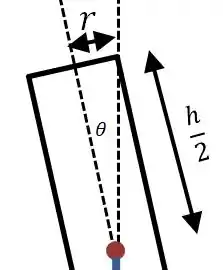
Então:
Resposta
(a) O topo deve se inclinar por uma distância adicional de .
(b) O ângulo da torre em relação à vertical seria de .