Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Exercícios - Ex. 2
Três espelhos planos interceptam-se em ângulos retos. Um feixe de laser atinge o primeiro deles em um ângulo com a normal (Figura 33.39). a) Mostre que, quando esse raio é refletido pelos outros dois espelhos e cruza o raio original, o ângulo entre esses dois raios será . b) Para que ângulo os dois raios serão perpendiculares quando se cruzarem?
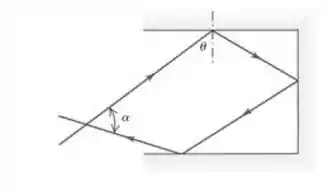
Passo 1
a)
Vamos lá! Lembrando que o ângulo incidente é igual ao ângulo refletido, teremos isso:
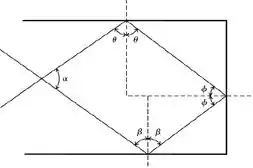
Daí já podemos tirar algumas relações:
Essas relações vem da soma dos ângulos internos de um triângulo ser beleza?
Passo 2
Tá, mas e o
Então, vamos olhar para o quadrilátero formado pelos raios. A soma dos ãnguos internos de um quadrilátero é . Então;
Mas vimos que:
Então:
Substituindo...
Agora é só arrumar:
Maravilha!
Passo 3
b) Os raios serão perpendiculares quando . Usando a relação do ítem anterior: