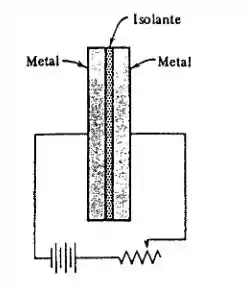
Use a lei de indução de Faraday para mostra que um buraco num supercondutor irá “prender” um fluxo magnético, isto é, , no buraco. Lembre-se que o campo elétrico em qualquer caminho no interior do supercondutor que contenha o buraco e também que o efeito Meissner não se aplica ao buraco.

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!

A lei da indução de Faraday afirma que qualquer fluxo magnético variável no tempo irá induzir uma força eletromotriz através de um circuito fechado de corrente

Aqui, é o fluxo magnético através do loop de corrente, o produto da área A delimitada pelo loop e o campo B entrando nele, e a força eletromotriz é a tensão induzida pela taxa de variação do fluxo no tempo. Se a área for considerada sobre um buraco em um supercondutor, o fluxo através dela não é excluído por meio do efeito Meissner, pois está dentro do supercondutor. Além disso, o supercondutor imediatamente circundando o buraco é essencialmente um circuito através do qual um loop de corrente pode fluir. Então, qualquer mudança no fluxo através do orifício irá induzir uma força eletromotriz dentro do supercondutor que circunda o orifício. No entanto, o campo elétrico dentro do supercondutor deve ser zero também. Um campo elétrico E é gerado por um potencial não uniforme V por seu gradiente negativo.