Use os resultados dos exemplos 5-5, 5-6 e 5-7 para calcular a probabilidade de encontrar uma partícula, no estado de menor energia de um oscilador harmônico simples quântico, entre os limites clássicos do movimento.
Passo 1
Fala galerinha, beleza?
No exemplo 5-7 foi encontrada a função de onda normalizada para o estado fundamental do oscilador harmônico simples:
Para calcular a probabilidade, precisamos primeiro da densidade de probabilidade dada por
O termo temporal sumiu pois
Assim, a probabilidade pedida vai ser dada pela integral
Passo 2
Os limites de integração foram obtidos no item (c) do problema 3:
Assim,
Vamos definir uma variável:
Assim, temos
Quando , temos . Já para , temos . Portanto, a integral fica:
Ou ainda,
Viu que lindo? Eliminamos completamente todas as constantes físicas!
Passo 3
Já vou adiantar para você que é impossível calcular a integral na mão! Vamos usar o WOLFRAM para resolver o problema...
O que você precisa digitar é
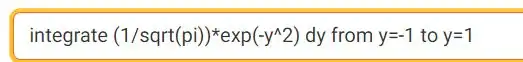
Fazendo isso, ele retorna
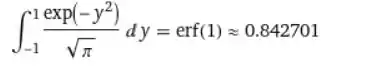
Portanto, a probabilidade pedida é