Uma viatura de polícia está viajando para o leste a 40,0 m/s ao longo de uma estrada reta, ultrapassando um carro antes de ele se mover para leste, a 30,0 m/s. A viatura tem uma sirene que está com mau funcionamento, travada a 1.000 Hz. (a) Qual seria o comprimento de onda no ar do som da sirene se a viatura da polícia estivesse em repouso? (b) Qual é o comprimento de onda na frente da viatura? (c) Qual é o comprimento de onda atrás da viatura? (d) Qual é a frequência ouvida pelo motorista que está sendo perseguido?
Passo 1
Alô Alô beleuzaaaaa, vamo pra mais uma resolução???
Então encoxxxtaaaa
- Para a situação de repouso, basta utilizarmos a equação fundamental da ondulatória. Assim teremos:
- Primeiramente, devemos lembrar da equação do efeito Doppler.
- Para um/a observador/a em repouso atrás da viatura, o esquema se torna:
- O esquema da observação está representado a seguir:
Passo 2
Na qual 340 m/s é a velocidade do som no ar, é a frequência da fonte, é a frequência observada, e é a velocidade da/o observador/a. Na equação o uso do sinal positivo ocorre quando o/a observador/a ou a fonte se move no sentido que liga o/a primeiro/o à segunda.
Na situação do item b, queremos calcular o comprimento de onda do som percebido por um/a observador/a em repouso na frente da viatura, como mostra a figura seguinte:
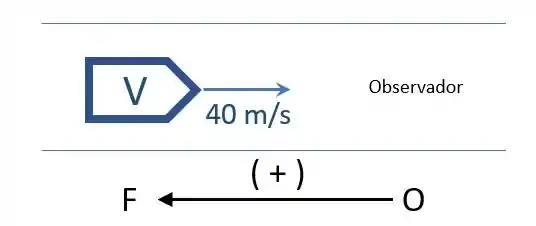
Sendo assim:
Porém:
Passo 3
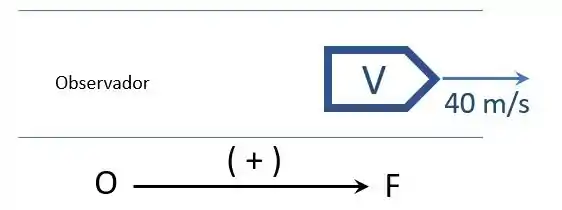
Sendo assim:
Porém:
Passo 4
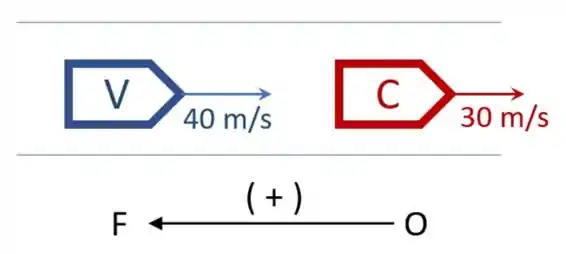
Assim, iremos obter