Você é um engenheiro trabalhando para uma empresa de manufatura. Você está projetando um mecanismo que usa um cabo para arrastar blocos de metal pesados por uma distância de ao longo de uma rampa inclinada em acima da horizontal. O coeficiente de atrito cinético entre esses blocos e a inclinação é . Cada bloco tem uma massa de . O bloco será colocado na parte inferior da rampa, o cabo será preso e o bloco receberá um empurrão momentâneo para contornar o atrito estático. O bloco, então, deve acelerar a uma taxa constante para ser movido pelos em . O cabo é feito de uma corda de fios e paralelo à superfície da rampa. A tabela oferece a tensão de ruptura do cabo em função de seu diâmetro; a tensão de carga segura, que é da tensão de ruptura; e a massa por metro linear do cabo:

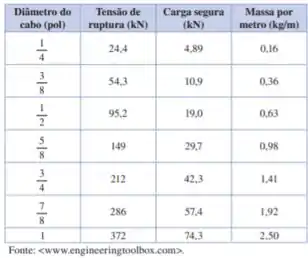
(a) Qual é o diâmetro mínimo do cabo que poderá ser usado para fazer subir um bloco na rampa sem ultrapassar o valor da carga segura da tensão no cabo? Ignore a massa do cabo e selecione o diâmetro dentre os listados na tabela. (b) Você precisa conhecer os valores da carga segura para os diâmetros que não estão na tabela, de modo que formule a hipótese de que a tensão de ruptura e o limite de carga segura são proporcionais à seção transversal do cabo. Desenhe um gráfico que teste essa hipótese e discuta sua exatidão. Qual é a sua estimativa do valor da carga segura para um cabo com diâmetro de pol? (c) O coeficiente de atrito estático entre o bloco e a rampa é , que é quase o dobro do valor do coeficiente de atrito cinético. Se o mecanismo emperrar e o bloco parar no meio da rampa, qual é a tensão no cabo? Ela é maior ou menor que o valor de quando o bloco está se movendo? (d) A tensão real no cabo, em sua extremidade superior, é maior ou menor que o valor calculado quando você ignora a massa do cabo? Se o cabo tem de extensão, é correto ignorar sua massa?

Agora vamos desenhar as forças que agem sobre o bloco enquanto ele sobe:

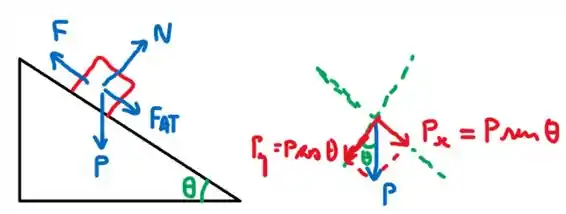
Como o bloco sobe, a força de atrito cinético aponta no sentido descendente do plano inclinado. Já fiz a decomposição do peso de modo que

Aplicando a segunda lei de Newton na direção do movimento:

Logo,

Portanto,

Substituindo os valores:

Fazendo as contas, achamos

Olhando na tabela, vemos que o primeiro fio cuja tensão de segurança supera esses é o fio cuja diâmetro é .

No item (b), devemos verificar a hipótese se a tensão de ruptura é proporcional a seção transversal do fio. Para isso, devemos lembrar que a área da seção transversal é proporcional ao diâmetro ao quadrado, de modo que definindo uma variável

devemos esperar um comportamento do tipo

Com isso, vamos fazer um gráfico de em função de , cujos dados são mostrados na tabela:

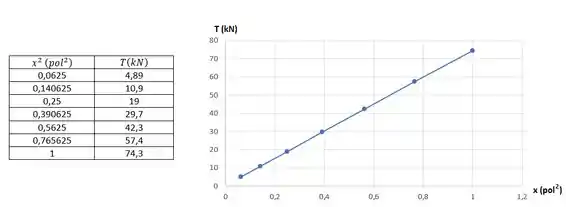
Observamos que uma reta ajusta muito bem os pontos, de modo que a hipótese levantada é verificada! Para um diâmetro com , temos . Do gráfico, podemos estimar uma tensão próxima de

Agora vamos para o item (c)! Temos que considerar a situação estática, de modo que

Logo,

Repare que agora estamos usando o atrito estático. Podemos escrever ainda:

Portanto,

Fazendo as contas,

Essa tensão é maior que a tensão quando o bloco está se movendo na situação do item (a).

Considerando a massa do cabo, a tensão na extremidade superior será sempre maior que a tensão que calculamos nos itens acima, pois além da massa dos blocos, teríamos que considerar a massa do cabo, o que aumentaria a força necessária para fazer o sistema acelerar.

Observe que para um comprimento , a massa do cabo mais grosso será

Note que essa é a maior massa possível que um cabo pode ter no problema e que essa massa é bem menor que a massa do bloco, de modo que podemos ignorá-la sem muitos problemas...

Caso a massa do cabo se aproximasse um pouco mais da massa do bloco, aí teríamos que tomar um pouco mais de cuidado!