Dois blocos de massas e são colocados sobre uma mesa em contato um com o outro, como discutido no Exemplo 4.5 e mostrado na Figura Ativa 4.13a. O coeficiente de atrito cinético entre o bloco de massa e a mesa é , e entre o bloco de massa e a mesa é . A força horizontal de módulo é aplicada ao bloco de massa . Queremos encontrar , o módulo da força de contato entre os blocos.
- Desenhe diagramas mostrando as forças em cada bloco.
- Qual é a força resultante no sistema de dois blocos?
- Qual é a força resultante que age em ?
- Qual é a força resultante que age em ?
- Escreva a Segunda Lei de Newton na direção para cada bloco.
- Resolva as duas equações com duas incógnitas para a aceleração dos blocos quanto às massas, a força aplicada , os coeficientes de atrito e .
- Encontre o módulo da força de contato entre os blocos com relação às mesmas quantidades.
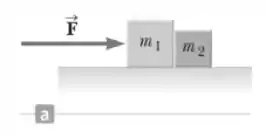
Figura Ativa 4.13a
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo e bora!
Letra a:
Os diagramas de corpo livre estão abaixo:
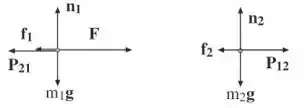
As forças verticais somam zero porque os blocos se movem em uma superfície horizontal; portanto, para cada bloco:
O atrito cinético é:
E
O atrito cinético é:
Passo 2
Letra b:
A força resultante no sistema dos blocos seria igual à magnitude da força, F, menos a força de atrito em cada bloco. Os blocos terão a mesma aceleração.
Passo 3
Letra c:
A força resultante na massa, , seria igual à força, F, menos a força de atrito em e a força , como identificado no diagrama do corpo livre.
Passo 4
Letra d:
A força resultante na massa, , seria igual à força, , menos a força de atrito em conforme identificado no diagrama de corpo livre.
Passo 5
Letra e:
Os blocos são empurrados para a direita pela força F, então o atrito cinético f atua em cada bloco à esquerda. Cada bloco tem a mesma aceleração horizontal, . Cada bloco exerce uma força igual e oposta no outro, então essas forças têm a mesma magnitude :
E
Passo 6
Letra f:
Adicionando as duas equações acima dos componentes x, encontramos:
Passo 7
Letra g:
Da equação do componente x para o bloco 2, temos:
Vemos que quando os coeficientes de atrito são iguais, , a magnitude P é independente do atrito.
Resposta
- A força resultante no sistema dos blocos seria igual à magnitude da força, F, menos a força de atrito em cada bloco. Os blocos terão a mesma aceleração.
- A força resultante na massa, , seria igual à força, F, menos a força de atrito em e a força , como identificado no diagrama do corpo livre.
- A força resultante na massa, , seria igual à força, , menos a força de atrito em conforme identificado no diagrama de corpo livre.
- Ver resolução