Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 3.Problemas - Ex. 78
Você é membro de uma equipe de geólogos na África Central. Sua equipe chega a um rio largo que está correndo para o leste. Você precisa determinar a largura do rio e a velocidade atual (a velocidade da água em relação ao solo). Você tem um pequeno barco com um motor de popa. Medindo o tempo gasto para atravessar um lago em que não há correnteza, você calibrou o acelerador para a velocidade do barco em águas paradas. Você define o acelerador de modo que a velocidade do barco em relação ao rio seja constante, a 6,00 m/s. Atravessando o rio rumo ao norte, você chega à margem oposta em 20,1 s. Para a viagem de volta, você muda a aceleração para que a velocidade do barco em relação à água seja 9,00 m/s. Você atravessa rumo ao sul de uma margem para a outra e atravessa o rio em 11,2 s. (a) Qual é a largura do rio e qual é a velocidade atual? (b) Com o acelerador preparado de modo que a velocidade do barco em relação à água seja 6,00 m/s, qual é o menor tempo em que você poderia atravessar o rio, e onde você aportaria na outra margem?
Passo 1
Este é um problema de adição de vetores. O barco se move em relação à água e a água se move em relação à terra. Nós sabemos a velocidade do barco em relação à água e o tempo para o barco ir diretamente do outro lado do rio, e a partir dessas coisas, queremos descobrir o quão rápido a água está se movendo e a largura do rio.
Para ambas as viagens do barco, , onde os subscritos se referem ao barco, terra e água. A velocidade do barco em relação à terra é , onde d é a largura do rio e t é o tempo de atravessar o rio, que é diferente nas duas travessias.
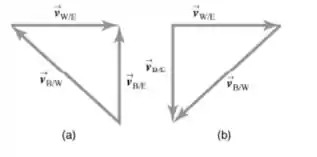
A figura mostra uma soma vetorial para a primeira viagem e para a viagem de volta.
Passo 2
Letra a:
Usando teorema de Pitágoras, temos:
Para a primeira viagem:
Para a volta:
Resolvendo as equações:
E podemos arredondar para 90.5m (largura do rio) e , arredondando para 3.97m/s (velocidade da correnteza).
Passo 3
Letra b:
O tempo mais curto é quando o barco se move perpendicularmente à corrente, que é para o norte, como vemos na figura abaixo:
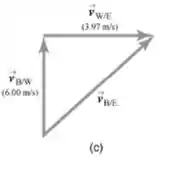
O tempo para cruzar é . A distância x que você viaja é .
Resposta
- E podemos arredondar para 90.5m (largura do rio) e , arredondando para 3.97m/s (velocidade da correnteza).
- O tempo para cruzar é . A distância x que você viaja é .