Exercícios de Movimento Relativo Bidimensional - Lista de Exercícios Resolvida
Questão 1
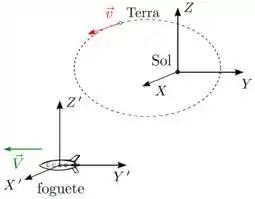
Vista de um referencial fixo nas escretas e centrado no Sol, a Terra tem vetor velocidade dado em um certo instante por e um foguete em translação tem velocidade constante , como mostra a figura. Considerando o foguete como um referencial com eixos coordenados , , e de mesmas direções e sentidos que os respectivos eixos , e , o vetor velocidade da Terra relativo a ele é
Questão 2
Um ônibus (ônibus 1) trafega com velocidade em relação a Terra. Outro ônibus (ônibus 2) se aproxima do ônibus 1 com velocidade de , também em relação à Terra.
- Qual a velocidade do ônibus 1 em relação ao ônibus 2?
- Qual é, aproximadamente, o módulo dessa velocidade?
Questão 3
Um carro move-se com velocidade constante de 60 km/h. Começa a chover e o motorista observa que as gotas de água da chuva caem formando um ângulo de 30° com a vertical. Considerando que, em relação à Terra, as gotas caem verticalmente, qual a velocidade em que as gotas de água caem em relação ao carro?
a) 30√3 km/h.
b) 60 km/h.
c) 120 km/h.
d) 30 km/h.
e) 80km/h.
Ver solução completaQuestão 4
Duas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrita pelas funções posição , , e , onde a posição é medida em metros e o tempo em segundos. Considere a direção na horizontal e na vertical.
Determine os vetores posição e de cada partícula e o vetor posição relativa .
Para ,faça um esquema no plano cartesiano dos vetores posição e e do vetor posição relativa . Determine a distância entre as partículas.
Determine o(s) tempo(s) para o(s) qual(is) as duas partículas colidem.
Determine a velocidade relativa, , no(s) instante(s) no(s) qual(is) as partículas colidem.
Ver solução completaQuestão 5
Um rio de 200 m de largura corre com uma velocidade uniforme de através de uma floresta, na direção oeste. Um explorador deseja sair de uma pequena clareira na margem sul e atravessar o rio em um barco a motor que se move com uma velocidade escalar constante de em relação à água. Existe uma outra clareira na margem norte, rio acima a partir de um ponto da margem sul, exatamente em frente à clareira. Em que direção o barco deve ser apontado para viajar em linha reta e chegar à clareira da margem norte? Quanto tempo o barco leva para atravessar o rio e chegar à clareira?
Ver solução completaQuestão 6
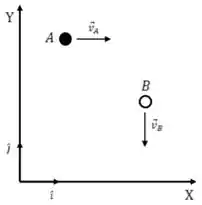
Duas partículas e se movem ao longo do eixo e , respectivamente, com velocidades constantes e . Em elas estão nas posições: , .
Esboce a situação descrita acima no plano no instante .
Escreva algebricamente (usando versores indicados no enunciado) o vetor posição de cada uma das partículas.
Determine o vetor que representa a posição relativa da partícula com respeito à partícula , como função do tempo.
Determine o vetor velocidade relativa entre essas duas partículas.
Ver solução completaQuestão 7
Um ciclista trafega com velocidade em relação a um observador em repouso no solo. Outra ciclista, que trafega com rapidez no sentido negativo do eixo x, observa o primeiro. Qual a velocidade do primeiro ciclista no referencial da segunda?
Ver solução completaQuestão 8
Observe a figura e leia atentamente o texto:
No instante , um carro, dirigido por Bruno , se encontra na esquina de um cruzamento enquanto que outro carro, dirigido por Ângela , está em uma rua a da esquina. Bruno viaja para Norte (eixo ) enquanto Ângela viaja para o Leste (eixo ). Em relação ao solo, as velocidades de Ângela e Bruno são constantes e têm mesmo módulo de .
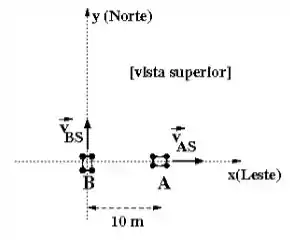
Escreva o vetor velocidade de Ângela em relação a Bruno .
Encontre o vetor posição de Ângela em relação a Bruno , em função do tempo.
Qual é a aceleração relativa de Ângela em relação a Bruno?
Ver solução completaQuestão 9
Um navio está ao norte e a leste do navio . O navio está navegando com uma velocidade constante de na direção sul; o navio navega com uma velocidade constante de em direção ao norte do leste.
Escreva uma expressão para o vetor posição de em relação à em função do tempo considerando o instante como o instante e que os navios estão nas posições iniciais descritas acima. (Sugestão: faça um desenho para orientá-lo na sua solução posicionando o navio na origem do sistema de coordenadas em ).
Dados:
Ver solução completaQuestão 10
Um observador parado no solo vê um pacote caindo de um avião, com velocidade de módulo igual a , mas que faz um certo ângulo com a vertical; considere a Terra um referencial inercial. Simultaneamente o piloto do avião, que voa na horizontal com velocidade constante, vê o mesmo pacote caindo na vertical, com velocidade de módulo igual a . O módulo da velocidade do avião em relação ao observador no solo é
Questão 11
Parado numa rua, embaixo de uma marquise, um homem vê as gotas de chuva caindo verticalmente com velocidade constante de módulo . Ao atravessar a rua (nivelada horizontalmente e plana) correndo em linha reta ele percebe que as gotas de chuva, durante a travessia, caem com um ângulo em relação à horizontal. Se ele atravessou a rua com velocidade de módulo constante em relação à Terra, a resposta correta que permite obter o ângulo , é
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 12
[2] Um avião, com frente apontada de oeste para leste, viaja com uma velocidade de em relação ao ar. Uma forte corrente de ar direcionada do sul para norte com velocidade de em relação à Terra atinge o avião constantemente.
(b) Faça um diagrama mostrando a relação entre os vetores velocidade do avião. Encontre o módulo da velocidade do avião em relação a um referencial na terra.
Ver solução completaQuestão 13
[3] Um corpo de massa , em trajetória unidimensional, possui velocidade cujo módulo varia no tempo de acordo com o gráfico abaixo. A posição inicial do corpo é .
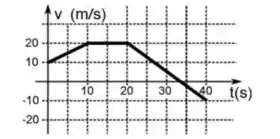
(a) Qual a posição do corpo em ?
Ver solução completaQuestão 14
[2] Um avião, com frente apontada de oeste para leste, viaja com uma velocidade de em relação ao ar. Uma forte corrente de ar direcionada do sul para norte com velocidade de em relação à Terra atinge o avião constantemente.
(a) Defina um sistema de coordenadas , e escreva as velocidades dadas do enunciado na forma vetorial.
Ver solução completaQuestão 15
[3] Um corpo de massa , em trajetória unidimensional, possui velocidade cujo módulo varia no tempo de acordo com o gráfico abaixo. A posição inicial do corpo é .
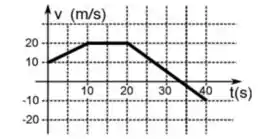
(b) Qual a força resultante que atua no corpo quanto ?
Ver solução completaQuestão 16
[3] Um corpo de massa , em trajetória unidimensional, possui velocidade cujo módulo varia no tempo de acordo com o gráfico abaixo. A posição inicial do corpo é .
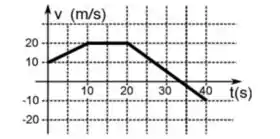
(c) Qual a posição do corpo quando Em que instante de tempo isso acontece?
Ver solução completaQuestão 17
Um atleta consegue correr em relação ao solo com velocidade e nadar com velocidade em relação à água. Ele quer atravessar um rio de corrente homogênea, cuja correnteza possui velocidade em relação às margens , saindo do ponto A e chegando ao ponto C, diretamente do outro lado da margem, como na figura. Como a temperatura da água está muito baixa, ele quer atravessar o rio, as águas o deslocam de seu objetivo, fazendo-o chegar do outro lado no ponto B. Considere as velocidades constantes e que .

1) que distância separa os pontos B, aonde ele chega na outra margem, e C, seu objetivo?
Ver solução completaQuestão 18
Um atleta consegue correr em relação ao solo com velocidade e nadar com velocidade em relação à água. Ele quer atravessar um rio de corrente homogênea, cuja correnteza possui velocidade em relação às margens , saindo do ponto A e chegando ao ponto C, diretamente do outro lado da margem, como na figura. Como a temperatura da água está muito baixa, ele quer atravessar o rio, as águas o deslocam de seu objetivo, fazendo-o chegar do outro lado no ponto B. Considere as velocidades constantes e que .
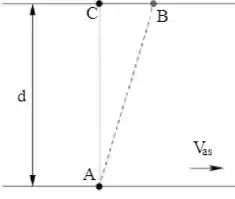
3) qual foi a velocidade vetorial média do atleta no percurso (módulo, direção e sentido)? Considerando a distância total percorrida, qual foi sua velocidade escalar média?
Ver solução completaQuestão 19
Duas partículas e se movem ao longo do eixo e , respectivamente, com velocidades constantes e . Em elas estão nas posições: , .
Esboce a situação descrita acima no plano no instante .
Escreva algebricamente (usando versores indicados no enunciado) o vetor posição de cada uma das partículas.
Determine o vetor que representa a posição relativa da partícula com respeito à partícula , como função do tempo.
Determine o vetor velocidade relativa entre essas duas partículas.
Ver solução completaQuestão 20
Duas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrita pelas funções posição , , e , onde a posição é medida em metros e o tempo em segundos. Considere a direção na horizontal e na vertical.
(a) Determine os vetores posição e de cada partícula e o vetor posição relativa .
(b) Para ,faça um esquema no plano cartesiano dos vetores posição e e do vetor posição relativa . Determine a distância entre as partículas.
(c) Determine o(s) tempo(s) para o(s) qual(is) as duas partículas colidem.
(d) Determine a velocidade relativa, , no(s) instante(s) no(s) qual(is) as partículas colidem.
Ver solução completaQuestão 21
Um navio está ao norte e a leste do navio . O navio está navegando com uma velocidade constante de na direção sul; o navio navega com uma velocidade constante de em direção ao norte do leste.
Escreva uma expressão para o vetor posição de em relação à em função do tempo considerando o instante como o instante e que os navios estão nas posições iniciais descritas acima. (Sugestão: faça um desenho para orientá-lo na sua solução posicionando o navio na origem do sistema de coordenadas em ).
Ver solução completaQuestão 22
A posição de um objeto medida por um observador , relativa a um sistema de coordenadas, é dada por . A posição deste mesmo objeto medida por um observador , relativa a outro sistema de coordenadas é dada por .
a) Mostre que a aceleração do objeto é a mesma medida por ambos observadores.
b) Determine os vetores posição e velocidade medidos pelo observador , relativos ao observador .
Ver solução completaQuestão 23
Duas escadas rolantes estão dispostas como mostra a figura. O ângulo de elevação de cada escada, em relação a horizontal é o mesmo. As escadas movimentam os degraus com velocidades constantes de mesmo módulo , medidas em relação a um referencial fixo na Terra. Em um dado instante, duas pessoas e entram simultaneamente nas escadas, como mostra a figura, e ao entrarem permanecem paradas em relação aos respectivos degraus. Seja um referencial fixo em e em translação relativa ao referencial da Terra. O módulo da velocidade de em relação enquanto e estão nas escadas é
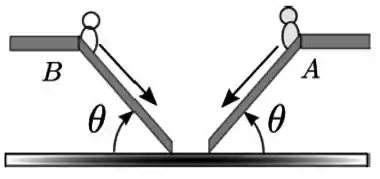
(a)
(b)
(c) não é constante
(d)
(e)
Ver solução completaQuestão 24
As águas de um rio correm a uma velocidade de . Uma lancha consegue se locomover a uma velocidade de em relação à água. Considerando que o rio tem uma largura de metros, e a lancha ajusta a direção da sua trajetória de forma a cruzar o rio perpendicularmente às suas margens, em quanto tempo ela chega ao outro lado?
Questão 25
Indique a alternativa que melhor completa a frase: "No movimento de um projétil...
(a) ...a aceleração no eixo horizontal depende da aceleração no eixo vertical.”
(b) ...a aceleração no eixo vertical depende da aceleração no eixo horizontal.”
(c) ...o movimento no eixo horizontal depende do movimento no eixo vertical.”
(d) ...o movimento no eixo vertical depende do movimento no eixo horizontal.”
(e) ...os movimentos horizontal e vertical são independentes.”
Ver solução completaQuestão 26
Parte I. Um estudante de física está dentro de um carro que segue a uma velocidade constante de na direção norte sob uma forte chuva que bate no carro da direção noroeste ( a oeste do norte) com velocidade constante de . Assinale as afirmativas verdadeiras sobre a velocidade do estudante em relação à chuva:
(a) seu módulo é igual a .
(b) sua direção é para a norte do leste.
(c) seu módulo é igual a .
(d) sua direção é para a sul do oeste.
(e) nenhuma das respostas é verdadeira.
Parte II. Suponha agora que dois pássaros, buscando abrigo contra a chuva, são vistos pelo estudante no carro: um pássaro () voando com velocidade constante de na direção sudeste ( ao sul do leste) e outro pássaro () voando acelerado em uma direção desconhecida. O estudante determina a equação da trajetória do pássaro dada por: . Determine , a velocidade do pássaro em relação ao pássaro .
Ver solução completaQuestão 27
Em um trecho retilíneo de um rio as águas têm velocidade relativa às margens constante e a mesma em todos os pontos do trecho do rio. Um piloto deseja atravessar o rio de modo que a velocidade de seu barco relativa às margens tenha o mesmo módulo que a velocidade das águas relativas às margens, . Além disso, ele deseja seguir uma trajetória retilínea de um ponto da margem até o ponto diretamente em frente a na margem oposta, como indica a figura. Podemos afirmar que o piloto deve imprimir ao barco uma velocidade , relativa às águas de módulo
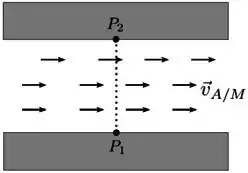
- ;
- ;
- ;
- ;
- ;
Questão 28
Um jogador de handebol se desloca com velocidade de na direção perpendicular à linha de fundo da quadra adversária. Ele é capaz de lançar a bola com velocidade de módulo em relação a ele próprio. Exatamente antes de tocar a linha de fundo ele lança a bola de maneira que ela continue em jogo. No referencial do jogador, qual deve ser o ângulo mínimo com que o ele deve fazer o lançamento para que isso aconteça? Dê o valor do ângulo em relação à direção da corrida.
(a) 90 graus.
(b) zero.
(c) 120 graus.
(d) 180 graus.
(e) 60 graus.
Ver solução completaQuestão 29
. Um nadador tenta atravessar um rio de metros de largura, nadando a . O rio tem
uma correnteza de paralela às margens. Se o nadador quer chegar à margem
oposta na mesma altura de onde saiu, quanto tempo levará para cruzar o rio? Utilize a
aproximação .
Ver solução completaQuestão 30
Um rio de de largura flui com rapidez de . Um barco atravessa o rio de um ponto numa margem para o ponto na margem oposta, perpendicular à correnteza, em . Qual é a rapidez do barco em relação à água?
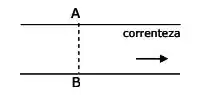
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 31
Um homem a bordo de um bote a remo quer atravessar o canal entre São Sebastião e Ilha Bela no litoral norte de São Paulo de modo que a menor distância, que é de 3,0 km, seja percorrida. O homem consegue imprimir uma velocidade de módulo 2,0 m/s em relação à água. Considerando que no dia da travessia a correnteza no canal tem velocidade de 1,0m/s na direção perpendicular à direção da menor distância, a travessia demora:
Questão 32
Um carro sobe uma ladeira em linha reta com velocidade constante em relação a um referencial fixo ao chão da ladeira; considere a Terra como um referencial inercial. Uma pessoa num helicóptero observa que a velocidade do carro em relação a ele é zero. Qual destas afirmações em relação ao referencial do helicóptero é verdadeira?
- A aceleração do helicóptero em relação ao referencial fixo do chão é diferente de zero
- O referencial do helicóptero é inercial
- As Leis de Newton não são aplicáveis nesse referencial
- Como a velocidade do helicóptero não é dada não é possível saber se o referencial do helicóptero é inercial ou não
- Nenhuma das respostas anteriores
Questão 33
Parte II - Duas rodovias se cruzam conforme a figura.
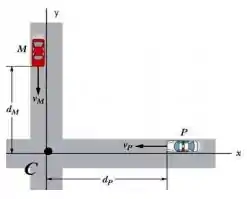
Um carro de polícia P se dirige para o cruzamento, estando distante do ponto C, com o mostrador do velocímetro indicando . Um outro carro M se move pela outra rodovia na direção do ponto de cruzamento, encontrando-se a uma distância , com velocidade escalar .
- Obtenha a velocidade do carro de polícia em relação ao carro M usando a notação de vetores unitários cartesianos.
- No instante mostrado na figura, determine o ângulo entre a reta que liga os dois carros e a velocidade relativa obtida no item (a) anterior.
Questão 34
Uma bola é lançada horizontalmente pela janela de um carro em movimento, perpendicularmente em relação à direção do movimento do carro. A velocidade do carro em relação ao chão é de , e a bola é lançada a em relação ao lançador. Ignorando a resistência do ar, qual é aproximadamente a velocidade da bola em relação ao chão?
a)
b)
c)
d)
e)
Ver solução completaQuestão 35
Um carro desce livremente por uma ladeira íngrime, com inclinação de , sem atrito. O motorista vê uma esfera cair livremente. Qual a aceleração relativa da esfera, no referencial do motorista, em termos da aceleração gravitacional?
Dica: aceleração da esfera no referencial da ladeira
Dado: .
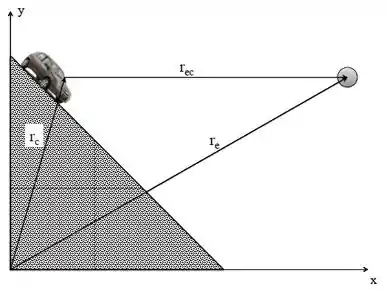
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 36
Parte II:
Uma partícula P se move com velocidade escalar constante sobre uma circunferência de raio (figura abaixo) e completa uma volta a cada . A partícula passa pelo ponto no instante . Nesse mesmo instante um atleta A passa pelo mesmo ponto com velocidade constante, correndo ao longo do eixo . O ponto designa a origem de um referencial () em repouso em relação ao solo. Expresse os resultados em função dos vetores unitários.
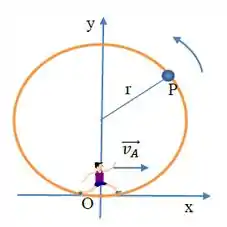
(a ) Encontre a posição da partícula em relação a , nos instantes e .
(b ) Obtenha o deslocamento da partícula entre 𝑒 .
(c ) Calcule a velocidade da partícula no instante .
(d ) Determine a velocidade da partícula em relação ao atleta no instante . Admita que o atleta A possui a mesma velocidade da partícula P na origem do referencial .
Ver solução completaQuestão 37
Observe a figura e leia atentamente o texto:
No instante , um carro, dirigido por Bruno , se encontra na esquina de um cruzamento enquanto que outro carro, dirigido por Ângela , está em uma rua a da esquina. Bruno viaja para Norte (eixo ) enquanto Ângela viaja para o Leste (eixo ). Em relação ao solo, as velocidades de Ângela e Bruno são constantes e têm mesmo módulo de .
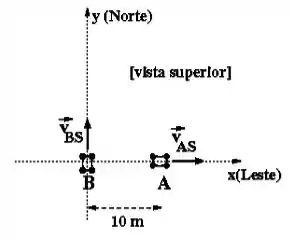
a) Escreva o vetor velocidade de Ângela em relação a Bruno .
b) Encontre o vetor posição de Ângela em relação a Bruno , em função do tempo.
c) Qual é a aceleração relativa de Ângela em relação a Bruno?
Ver solução completaQuestão 38
Uma garota deseja cruzar um rio nadando diretamente ao ponto oposto na outra margem, como mostrado na figura. Ela pode nadar a uma velocidade de em relação à água e o rio está fluindo a. Em que ângulo em relação à linha que une o ponto de largada (Start) e o ponto de chegada (Finish) ela deve nadar?
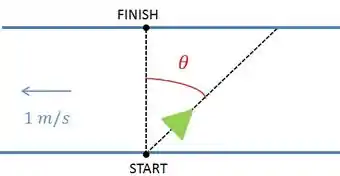
a.
b.
c.
d.
e.
Ver solução completaQuestão 39
Considere o ponto em dois referenciais e , nos quais as coordenadas no instante são e , com as posições dadas em metros. No instante , temos que e . Considere que a velocidade entre os referenciais e é constante e escreva-a em formato vetorial. Ela é:
a.
b.
c.
d.
e.
Ver solução completaQuestão 40
Uma esteira rolante elétrica tem extensão de 20 metros e se move a . Duas crianças, Odilon e Kellen, resolvem apostar uma corrida de ida e volta no trajeto da esteira, sendo que Odilon vai e volta por fora da esteira e a Kellen vai e volta em cima dela. Se ambas as crianças conseguem correr a uma mesma velocidade de , é correto afirmar que:
- O Odilon vence a corrida com uma vantagem de .
- A Kellen vence a corrida com uma vantagem de .
- Os dois chegam ao mesmo tempo.
- O Odilon vence a corrida com uma vantagem de .
- A Kellen vence a corrida com uma vantagem de .
Questão 41
Dois aviões estão estacionando em um aeroporto. João está no avião se movendo no sentido sul. Samanta está no avião , movendo-se para oeste. Os dois aviões partem de posições próximas um ao outro. Em que sentido João vê o avião de Samanta se movendo?
(a) Oeste.
(b) Sul.
(c) Entre o Norte e o Oeste.
(d) Leste.
(e) Entre o Sul e o Leste.
Ver solução completaQuestão 43
O GPS de um avião indica que ele está apontado para leste e seu indicador de velocidade em relação ao ar marca . Contudo, um forte vento constante cuja velocidade é de em relação ao solo passa a soprar para o norte. Se o piloto deseja continuar a voar para leste, como indica o GPS, para que direção ele deve apontar o avião?
a) em direção nordeste
b) em direção sudoeste
c) em direção noroeste
d) em direção sudeste
Ver solução completaQuestão 44
Um homem parado embaixo de uma marquise em uma rua nivelada horizontalmente vê as gotas de chuva caindo verticalmente com velocidade constante de módulo . Ao atravessar a rua correndo em linha reta ele percebe que as gotas de chuva, durante a travessia, caem com um ângulo em relação à horizontal. Se ele atravessou a rua com velocidade de módulo constante em relação à Terra, a resposta correta que permite obter o ângulo , é:
(a) )
(b)
(c)
(d)
(e)
Ver solução completaQuestão 45
Um atleta consegue correr em relação ao solo com velocidade e nadar com velocidade em relação à água. Ele quer atravessar um rio de corrente homogênea, cuja correnteza possui velocidade em relação às margens , saindo do ponto A e chegando ao ponto C, diretamente do outro lado da margem, como na figura. Como a temperatura da água está muito baixa, ele quer atravessar o rio, as águas o deslocam de seu objetivo, fazendo-o chegar do outro lado no ponto B. Considere as velocidades constantes e que .
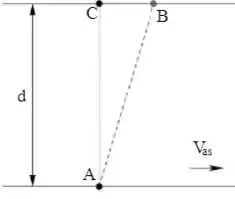
2) assim que chega em B, o atleta corre pelo solo, com a velocidade , para ir até C. Qual é o tempo total gasto pelo atleta desde o instante que saiu de A até chegar em C, seu objetivo?
Ver solução completaQuestão 46
O seguinte enunciado refere-se às questões e :
Um avião consegue viajar a uma velocidade de módulo em relação ao ar que o circunda. Tal avião quer seguir para o norte, enfrentando um vento de velocidade , onde a direção aponta para o leste e a direção aponta para o norte e é uma constante.
7. Para qual direção o avião deve apontar?
a) diretamente para o norte.
b) Para o nordeste, formando um ângulo de 26° em relação ao norte.
c) Para o nordeste, formando um ângulo de 30° em relação ao norte.
d) Para o noroeste, formando um ângulo de 30° em relação ao norte.
e) Para o noroeste, formando um ângulo de 26° em relação ao norte.
8. Qual é a velocidade de cruzeiro do avião (em relação ao chão).
a)
b)
c)
d)
e) nenhuma das anteriores.
Ver solução completaQuestão 47
Duas partículas e movem-se no plano horizontal , respectivamente com velocidades e constantes. A direção do movimento de é perpendicular ao eixo e a direção do movimento de é perpendicular ao eixo ; vide a figura abaixo. Seja a velocidade de com relação a a opção correta é:
- , pois é perpendicular a
- Todas as opções acima estão erradas
Questão 49
Um rio de um 1 km de largura tem uma correnteza de velocidade 1,5 Km/h. Um homem atravessa o rio de barco, remando a uma velocidade de 2,5 Km/h em relação à água.
a) Qual é o tempo mínimo que leva para atravessar o rio?
b) Nas condições do item anterior, onde o homem desembarca?
c) Suponha agora que o homem quer chegar a um ponto diametralmente oposto na outra margem, e tem duas opções: remar de forma a atingi-lo diretamente, ou remar numa direção perpendicular à margem, sendo arrastado pela correnteza até além do ponto onde quer chegar, e depois caminhar de volta até lá. Se ele caminha a 6 km/h, qual das duas opções é mais vantajosa quanto ao tempo de percurso, e quanto tempo leva?
Ver solução completaQuestão 50
Os vetores posição de duas partículas são dados por:
A velocidade relativa da partícula 1 em relação a partícula 2 no instante t=1s vale:
a)
b)
c)
d)
e) zero
Ver solução completaQuestão 51
Um barco encontra-se em repouso em relação à água de um rio. A correnteza do rio tem velocidade de em relação às margens, se movendo em direção ao norte. Uma pessoa anda dentro do barco para o leste, com velocidade de . Qual é a direção do movimento da pessoa em relação às margens? E qual o módulo de sua velocidade?
- Para o leste,
- Para o sudeste,
- Para o norte,
- Para o nordeste,
- Para o sudeste,
Questão 52
Um ciclista trafega com velocidade em relação a um observador em repouso no solo. Outra ciclista, que trafega com rapidez no sentido negativo do eixo x, observa o primeiro. Qual a velocidade do primeiro ciclista no referencial da segunda?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 53
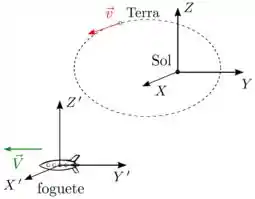
Vista de um referencial fixo nas estrelas e centrado no Sol, a Terra tem vetor velocidade dado em um certo instante por e um foguete em translação tem velocidade constante , como mostra a figura. Considerando o foguete como um referencial com eixos coordenados , , e de mesmas direções e sentidos que os respectivos eixos , e , o vetor velocidade da Terra relativo a ele é
Questão 55
A neve cai, verticalmente, com uma velocidade constante de . O motorista de um carro, viajando em linha reta numa estrada com uma velocidade de , vê os flocos de neve caírem formando um ângulo com a vertical. O valor deste ângulo é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 56
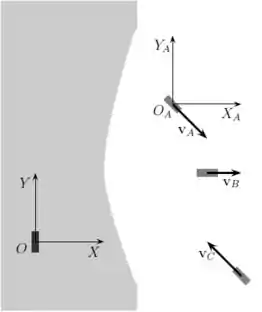
Em um lago tranqüilo três barcos , e têm velocidades respectivas , e ( uma constante dada), todas relativas ao referencial constituído por um ônibus estacionado na margem com um sistema de eixos , sendo na horizontal, conforme a figura. Considere o barco como um referencial com sistema de eixos , cada um deles com mesma direção e sentido dos respectivos eixos de . Em relação ao referencial do barco as velocidades do ônibus, do barco e do barco são, respectivamente,
- , e
- , e
- , e
- , e
- Nenhuma das respostas anteriores


