Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.2 - Ex. 11

Uma astronauta está dentro de um foguete com 2,25 × 10 6   k g que está subindo verticalmente a partir da plataforma de lançamento. Você deseja que esse foguete alcance a velocidade do som ( 331   m / s ) o mais rápido possível, mas os astronautas correm o perigo de desmaiar em uma aceleração maior que 4 g . (a) Qual é a propulsão inicial máxima que os motores desse foguete poderão ter de modo a evitar o desmaio? Comece com um diagrama do corpo livre para o foguete. (b) Que força, em termos do peso p da astronauta, o foguete exerce sobre ela? Comece com um diagrama do corpo livre para a astronauta. (c) Qual é o menor tempo necessário para que o foguete alcance a velocidade do som?

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente determinar (a) a força de propulsão máxima que o foguete pode ter, (b) a força que o foguete exerce sobre a astronauta e (c) o menor tempo necessário para que o foguete alcance a velocidade do som.

Então, vamos desenhar um diagrama de corpo livre para a situação e aplicar a segunda lei de Newton para analisar as forças do sistema, considerando que temos uma aceleração constante, pois temos força constante.

Os diagramas de corpo livre estão abaixo e vão nos ajudar na questão!!

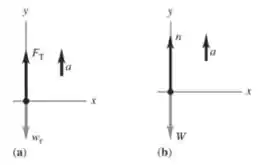
Onde F T é o empuxo e n é a força normal que o foguete exerce sobre o astronauta. E a velocidade do som é v = 331   m / s . Vamos usar a segunda lei para as forças verticais, na forma:

∑ F y = m a y  

E a equação cinemática, v = v 0 + a t , para determinar o tempo na velocidade do som. Vamos lá!

Passo 2

A partir do diagrama de corpo livre da figura (a), teremos no foguete:

F T - w t = m a

Como a = 4 g   é a maior aceleração possível e o peso é dado por w t = m g , teremos:

F = m 5 g

Então, substituindo o valor da massa do foguete e da aceleração da gravidade g , temos:

F = 2 , 25 × 10 6 k g 5 9 , 80 m s 2

F = 1 , 10 × 10 8   N

Passo 3

b) Agora vamos considerar o diagrama de corpo livre do astronauta na figura (b), vista no passo 1 . Assim, temos:

n - w = m a

Considerando a = 4 g   e m = w g , vamos ter:

n = w + w g 4 g

Então, substituindo os valores, obtemos:

n = 5 w

Passo 4

c) Agora vamos considerar a velocidade inicial v 0 = 0 , a velocidade do som v = 331 m s   e a aceleração a = 4 g = 39 , 2   m / s 2 para calcularmos o tempo através da equação:

v = v 0 + a t

Isolando t na equação, vamos ter:

t = v - v 0 a

E substituindo os valores,

t = 331   m s 39 , 2   m s 2

Obtemos:

t = 8 , 4   s

O 8,4   s é provavelmente um tempo pouco realista para atingir a velocidade do som porque você não gostaria que seus astronautas estivessem à beira de um apagão durante um lançamento.

Valeu, galera! Até a próxima! 😉

Resposta

  1. 1 , 10 × 10 8   N
  2. 5 w
  3. 8 , 4 s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A resistência do ar sobre um paraquedas exerce uma força F a = 8,0 Nx s 2 m 2 v 2 , onde v é a velocidade da queda. Qual é a velocidade limite (velocidade máxima) de um paraquedista de massa igual a 6
Uma pedra cuja densidade é ρ = 2,5g / c m 3 afunda em um lago. Sabendo-se que a água exerce sobre a pedra uma força de empuxo para cima igual ao peso do volume de água deslocada pela pedra, e que a de
Um avião, cuja massa é de 50.000 kg, viaja na horizontal à velocidade constante de 720 km/h. Suas turbinas exercem um empuxo de 7,0x10 4 N na direção horizontal. Calcule a força que o ar exerce sobre
Um carro, cuja massa vale 1200 kg, viaja a 100 km/h quando o motorista pisa fortemente no freio. Então, o atrito do pneu com a pista faz uma força F a = 7,7 ∙ 10 3 N, que permanece constante durante a
O gás expelido de um foguete lançado para cima, na vertical, faz sobre ele uma força de empuxo igual a 120 × 10 3N . Sendo 3,0 toneladas a massa do foguete, calcule a sua aceleração.