Você utiliza um teslômetro (um dispositivo de efeito Hall) para medir o módulo do campo magnético em diversas distâncias a partir de um cabo de cobre cilíndrico, longo, retilíneo e grosso, conduzindo uma corrente grande e constante. Para excluir o campo magnético da Terra da medição, primeiro você zera o medidor. Depois, mede o campo magnético B nas distâncias x a partir da superfície do cabo e obtém estes dados:
(a) Você acredita, pelo que aprendeu no curso de física, que o campo magnético de um fio é inversamente proporcional à distância do fio. Portanto, espera que a quantidade Bx de seus dados seja constante. Calcule Bx para cada ponto de dados na tabela. Bx é constante para esse conjunto de medições? Explique. (b) represente os dados como x em função de 1/B. Explique por que esse gráfico fica próximo de uma linha reta. (c) Use o gráfico do item (b) para calcular a corrente I no cabo e o raio R do cabo.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui!
Bora!
Letra a:
Multiplicando as quantidades dadas na tabela do problema, obtemos os seguintes valores para em unidades de , começando com o primeiro par: . Como podemos ver, estes valores não são constantes.
No entanto, os últimos três valores são quase constantes. Portanto, não é verdadeiramente constante. A razão para isso é que x é a distância da área do cabo, não do centro.
Na fórmula , r é a distância do centro do cabo. Nesse caso, esperaríamos que fosse constante.
Para os últimos três pontos, parece que é quase constante. A razão para isso é que o
a fórmula adequada para o campo magnético deste cabo é:
Onde R é o raio do cabo.
À medida que x fica grande em comparação com e a magnitude se aproxima de
Passo 2
Letra b:
Abaixo temos o gráfico :
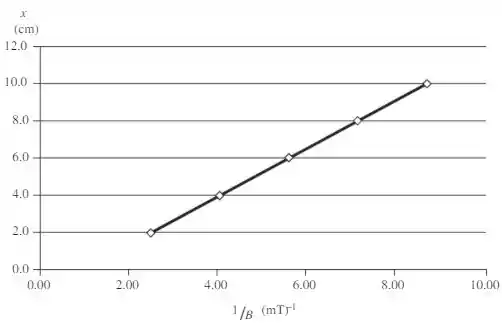
Passo 3
Letra c:
O melhor ajuste para este gráfico é:
A inclinação é:
Como a inclinação é , então:
E o intercepto em y é:
Resposta
- À medida que x fica grande em comparação com e a magnitude se aproxima de
- Ver gráfico