Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 62

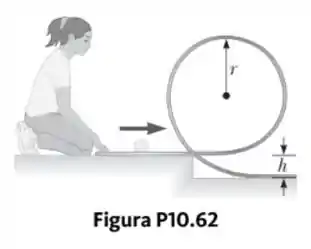
Uma bola de tênis é uma esfera oca com parede fina, posta para rolar sem escorregar a 4,03   m / s na seção horizontal da pista, como mostrado na Figura P10.62. Ela rola em torno da parte interna de um loop circular vertical de raio r   =   45,0   c m . Conforme a bola se aproxima da base do loop, o formato da pista desvia de um círculo perfeito de modo que a bola sai da pista em um ponto h   =   20,0   c m abaixo da parte horizontal.

  1. Encontre a velocidade da bola no topo do loop.
  2. Demonstre que a bola não cairá da pista no topo do loop.
  3. Encontre a velocidade da bola à medida que ela sai da pista na base.

    4. E Se?

  4. Suponha que o atrito estático entre a bola e a pista seja insignificante de modo que a bola deslize em vez de rolar. A velocidade seria maior, menor ou a mesma no topo do loop?
  5. Explique sua resposta para a parte (d).

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Há conservação de energia para o sistema:

1 2 m v 2 2 + 1 2 I ω 2 2 + m g y 2 = 1 2 m v 1 2 + 1 2 I ω 1 2 1 2 m v 2 2 + 1 2 2 3 m r 2 v 2 r 2 + m g y 2 = 1 2 m v 1 2 + 1 2 2 3 m r 2 v 1 r 2 5 6 v 2 2 + g y 2 = 5 6 v 1 2

v 2 = v 1 2 - 6 5 g y 2 = ( 4.03 m / s ) 2 - 6 5 9.80 m s 2 ( 0.900 m ) = 2.38 m s

Passo 2

Letra b:

A aceleração centrípeta no topo é:

v 2 2 r = ( 2.38 m / s ) 2 0.450 m = 12.6 m s 2 > g

Assim, a bola deve estar em contato com a pista, com a pista empurrando para baixo sobre ele.

Passo 3

Letra c:

1 2 m v 3 2 + 1 2 2 3 m r 2 v 3 r 2 + m g y 3 = 1 2 m v 1 2 + 1 2 2 3 m r 2 v 1 r 2

v 3 = v 1 2 - 6 5 g y 3 = ( 4.03 m / s ) 2 - 6 5 9.80 m s 2 ( - 0.200 m ) = 4.31 m s

Passo 4

Letra d:

1 2 m v 2 2 + m g y 2 = 1 2 m v 1 2 v 2 = v 1 2 - 2 g y 2 = ( 4.03 m / s ) 2 - 2 9.80 m s 2 ( 0.900 m ) = - 1.40 m 2 s 2

Passo 5

Letra e:

Este resultado é imaginário. No caso em que a bola não rola, a bola começa com menos energia cinética do que na parte (a) e chega ao topo do loop.

Resposta

  1. 2.38 m s
  2. Assim, a bola deve estar em contato com a pista, com a pista empurrando para baixo sobre ele.
  3. 4.31 m s
  4. - 1.40 m 2 s 2
  5. Este resultado é imaginário. No caso em que a bola não rola, a bola começa com menos energia cinética do que na parte (a) e chega ao topo do loop.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco de 12 cm de raio, que começa a girar em torno de seu eixo em t = 0 , gira com uma aceleração angular constante de 8,0r a d / s 2 . Em t = 5,0s , (a) qual é a rapidez angular do disco e (b) qu
Uma mesa giratória, girando a 33 r e v / m i n , é levada ao repouso em 26 s. Supondo constante a aceleração angular, encontre (a) a aceleração angular. Durante esses 26s , determine (b) a rapidez ang
Considere o pulsar do Caranguejo, discutido na Seção 9-2. Justifique a afirmativa de que a perda de energia rotacional é equivalente à potência emitida por 100000 estrelas. A potência total irradiada
Qual é a rapidez angular da Terra, em radianos por segundo, na rotação em torno de seu eixo?
Uma roda-gigante de 12m de raio completa uma volta a cada 27s . (a) Qual é a sua rapidez angular (em radianos por segundo)? (b) Qual é a rapidez linear de um passageiro? (c) Qual é a aceleração de um