P3 de Física 2- FIS1041 da PUCRIO - 2010.2

Uma caixa de isopor contendo de gelo a , troca calor com o meio ambiente a

uma taxa constante de . O calor de fusão da água a pressão atmosférica é .

Quanto tempo demora o gelo para se derreter completamente?

Que temperatura alcançaria a água se continuasse recebendo calor com a mesma taxa por um tempo igual ao calculado no item anterior? (o calor específico da água é .)

Titã, o maior satélite de Saturno, possui uma densa atmosfera de nitrogênio (). Em sua superfície a pressão é vezes a pressão atmosférica terrestre e a temperatura é .

Quantas moléculas por métro cúbico há na atmosfera da superfície de Titã?

Qual é a velocidade quadrática media dessas moléculas? (a massa molar das moléculas de é )

Três mols de um gás ideal monoatômico passam pelo ciclo termodinâmico descrito na figura( isobárico, isotérmico e isocórico):

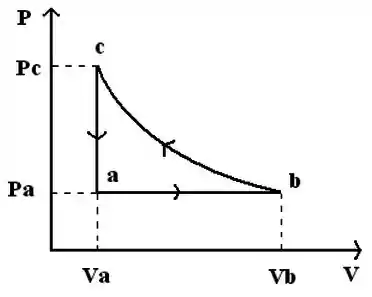
Dados , e , determine , e (tome e trabalhe com dois algarismos significativos).

Determine o trabalho realizado pelo sistema , o calor cedido ao sistema e a variação da energia interna para cada processo e preencha a tabela (justifique cada valor encontrado):

O ciclo considerado descreve uma máquina térmica ou um refrigerador? Justifique

Calcule a eficiência (se for máquina), ou coeficiente de desempenho (se for refrigerador), do ciclo.

Faça um gráfico do ciclo considerado.

O ciclo da figura abaixo representa a operaçãoo de um motor de combustão interna de gasolina (ciclo de Otto). Suponha que a mistura gasolina-ar é equivalente a mols de um gás ideal com .

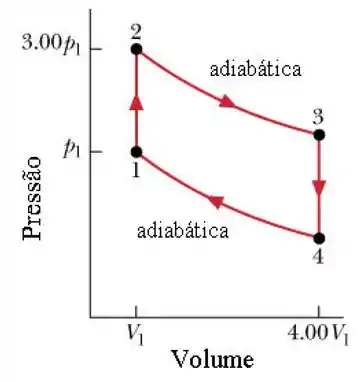
Determine as razões entre as temperaturas absolutas , e .

Determine as razões entre as pressões e .

Determine o trabalho total realizado no ciclo (em função de ).

Em que fase o calor é fornecido ao sistema? Calcule esse calor (em função de ).

Calcule a eficiência dessa máquina, supondo que todas as trocas de calor ocorrem com fontes externas ao sistema.

Determine a variação de entropia da substância de trabalho em cada fase do ciclo (em função de ).