Gases Ideais, Primeira Lei da Termodinâmica, Ciclos Termodinâmicos e Máquinas Térmicas
O ciclo da figura abaixo representa a operaçãoo de um motor de combustão interna de gasolina (ciclo de Otto). Suponha que a mistura gasolina-ar é equivalente a mols de um gás ideal com .
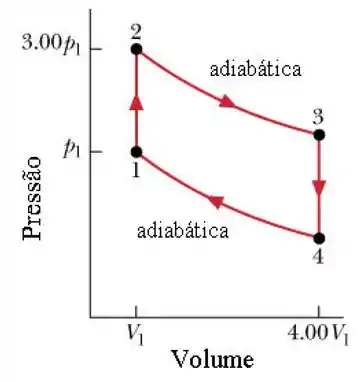
Determine as razões entre as temperaturas absolutas , e .
Determine as razões entre as pressões e .
Determine o trabalho total realizado no ciclo (em função de ).
Em que fase o calor é fornecido ao sistema? Calcule esse calor (em função de ).
Calcule a eficiência dessa máquina, supondo que todas as trocas de calor ocorrem com fontes externas ao sistema.
Determine a variação de entropia da substância de trabalho em cada fase do ciclo (em função de ).
Passo 1
Antes de atacar o problema, vamos primeiro extrair as informações que são dadas através da figura:
Para determinar as razões, vamos montar as equações, baseada na lei dos gases ideais, para dois pontos e depois dividir as duas para obter a razão! Ficou confuso? Se liga, então:
Para o ponto , temos:
Para o ponto , temos:
Agora é só dividir a equação do ponto pela equação do ponto :
Passo 2
Para o processo adiabático entre os pontos e , temos:
Fazendo as substituições, temos:
Passo 3
Analogamente, temos para o processo adiabático entre os pontos e :
Fazendo as substituições, temos:
Passo 4
Para determinar as razões entre as pressões, vamos fazer como fizemos no item anterior:
Para o ponto , temos:
Para o ponto , temos:
Lembrando que fizemos as substituições baseadas nas informações que extraímos da figura e das razões que achamos no item anterior!
Dividindo a equação para o ponto pela equação para o ponto , temos:
Passo 5
Vamos fazer o mesmo procedimento para os pontos e !
Para o ponto , temos:
Agor é só dividir a equação para o ponto pela equação para o ponto !
Passo 6
Vamos primeiro analisar a figura. Podemos perceber que o trabalho realizado entre e e entre e é zero pois são processos isovolumétricos!
Agora vamos para os processos adiabáticos. Nesses processos, sabemos que não há troca de calor, ou seja:
portanto, pela primeira lei da termodinâmica, temos:
Pela definição de energia interna, temos:
Precisamos agora determinar , que são os graus de liberdade do gás:
Passo 7
Para determinar , podemos utilizar a definição de
Como o valor de é dado, temos:
Passo 8
Agora podemos calcular o trabalho, para o processo , temos:
Substituindo e colocando as temperaturas em função de , temos:
Agora para o processo , temos:
Passo 9
Ou seja, para o ciclo, teremos:
Passo 10
Para determinar em que fase o calor é fornecido, vamos pensar da segunte maneira. Sabemos que nos processos adiabáticos não há troca de calor. Portanto devemos analisar apenas os processos e . Nesses processos, não é realizado nenhum trabalho, ou seja:
Podemos ver que no processo , a pressão aumenta a volume constante, aumentanto a temperatura, ou seja, a energia interna do sistema aumenta, para que isso aconteça, calor deve ser fornecido ao sistema. Portanto na fase foi fornecido calor ao sistema.
No processo vemos que a pressão diminue a pressão constante, diminuindo assim a temperatura, ou seja, a energia interna do sistema diminue, desse modo o sistema está rejeitando calor.
Passo 11
Vamos ao que interessa, que é calcular o calor fornecido no processo :
Substituindo e colocando a temperatura em função de , temos:
Passo 12
Para calcular a eficiência da máquina, vamos relembra da fórmula para a eficiência:
Substituindo os valores, temos:
Passo 13
Nos processos adiabáticos, temos que a variação de entropia é zero:
Para o processo , temos:
Substituindo por ,temos:
Substituindo os valores, temos:
Passo 14
Para o processo , podemos fazer o mesmo procedimento, no entanto, sabendo que a variação de entropia do ciclo deve ser zero, teremos que:
Resposta
; ;
;
; ;