(I) Um capacitor de placas paralelas circulares, no vácuo, está sendo carregado, como indica a figura abaixo. As placas têm raio e a corrente de condução nos fios no instante é igual a .
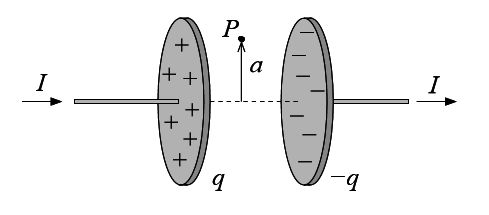
Calcule o campo magnético no ponto a uma distância do eixo do capacitor, conforme a figura. Dado: o campo elétrico dentro do capacitor é , onde é a densidade superficial de carga.
(II) O campo elétrico de uma onda que se propaga no vácuo é dada por , onde a constante . Use a lei de Faraday, , para calcular o campo vetorial desta onda.
Passo 1
(I)
Aplicando a lei de Ampère-Maxwell temos, já que a corrente circulada é nula:
Como a integral de é o comprimento da circunferência de raio :
Substituindo a área e o valor do campo elétrico:
Substituindo a densidade de carga superficial e sabendo que :
Passo 2
(II)
Como o campo só tem componente , a lei de Faraday se escreve como
Como estamos interessados na solução ondulatória podemos colocar . Basta resolver a EDO:
Se chamarmos uma variável auxiliar , tal que podemos escrever
Derivando a expressão de e como e :
Para saber temos que integrar!
Voltando da variável pra variável :
Resposta
(I)
(II)