A figura abaixo mostra um fio condutor retilíneo, conduzindo uma corrente
O fio é coplanar a uma bobina retangular com espiras compactas. A bobina possui resistência . O fluxo do campo magnético gerado pelo fio através de uma espira da bobina é dado por , onde não depende do tempo.
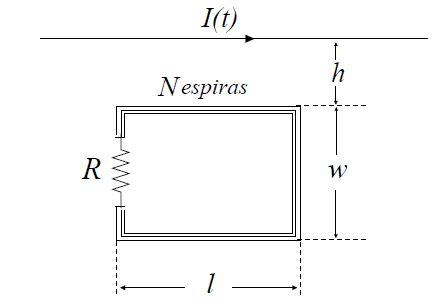
Calcule a potencia instantânea dissipada na bobina.
Calcule o fluxo e, através dele, determine o valor da constante em termos de , , e .
Passo 1
Calcule a potencia instantânea dissipada na bobina.
A potência dissipada na espira é dada por:
Então, o nosso trabalho aqui é calcular a induzida na espira . Para isso, teremos que recorrer à Lei de Faraday, dada por:
Como é o fluxo magnético através de uma espira, . Portanto:
Substituindo a expressão de dada pelo enunciado, teremos:
Substituindo a expressão de , teremos:
Agora, sim!
Finalmente, voltando para a potência, teremos:
Passo 2
Calcule o fluxo e, através dele, determine o valor da constante em termos de , , e .
Por definição, o fluxo magnético através de uma espira será:
Podemos simplificar isso para:
Onde é o campo magnético gerado pelo fio na espira, dado por:
E é o elemento infinitesimal da área. Nesse caso, .
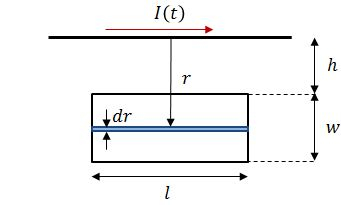
Onde . Portanto:
Integrando esse cara, teremos:
Passo 3
De acordo com o enunciado, , portanto:
Finalmente:
Resposta