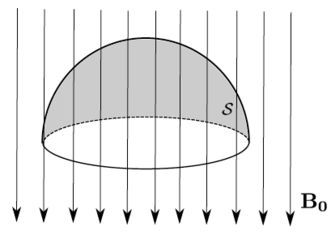
A figura abaixo mostra um hemisfério de raio imerso em uma região de um campo magnético constante de intensidade , que aponta perpendicularmente ao plano central do hemisfério. Considere uma superfície aberta formada apenas pela calota hemisférica. Podemos afirmar que a intensidade do fluxo de campo magnético através desta superfície vale:

7. 0

O fluxo do campo magnético é dado por

em que é uma superfície qualquer de contorno , ou seja, o fluxo de  será o mesmo através de qualquer superfície (aberta ou fechada!!) cujo contorno seja o mesmo. Um exemplo disso, é o caso deste problema: a superfície aberta da figura do enunciado tem o mesmo contorno da superfície plana circular de raio . Portanto, para calcularmos para esse caso, basta olharmos para a superfície plana de raio .

Sabemos que  neste caso é uniforme, o que significa que ele tem o mesmo valor em todos os pontos da superfície plana de raio . Além disso, o ângulo entre  e o elemento  é zero em todos os pontos desse plano, o que nos ajuda a simplificar a expressão para o fluxo:

Realizando a integral, teremos apenas a área e o fluxo magnético fica reescrito como