Um fio retilíneo infinitamente longo conduzindo uma corrente é parcialmente envolvido por uma espira semicilíndrica, como mostra a figura. A espira tem comprimento , raio e transporta uma corrente . O eixo da espira coincide com o do fio.

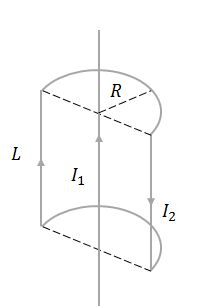
Calcule a intensidade do campo magnético produzido pelo fio em ;

Calcule a força magnética total exercida sobre a espira;

Se a corrente variar com o tempo, haverá induzida na espira? Justifique.

Calcule a força magnética total exercida sobre a espira;

Pra calcular a força total sobre a espira, precisamos calcular a força magnética sobre cada parte da espira. Então vamos começar dividindo a espira em 4 partes:

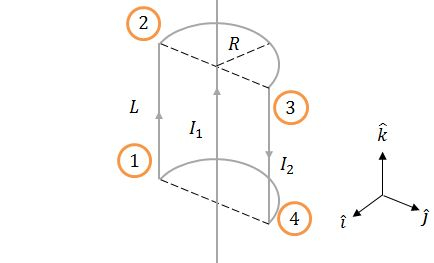
A força magnética sobre cada parte é dada por:

Para o caso de fios retilíneos, a força será dada por:

Onde o vetor tem a mesma direção e sentido da corrente .

Então o nosso trabalho aqui é calcular a força magnética em cada fio.

• Fio 1:



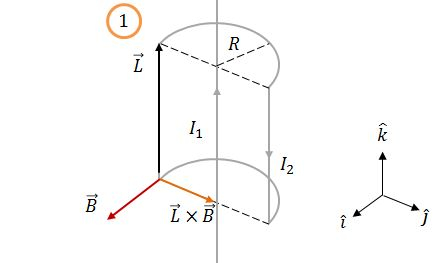
Assim, a força magnética sobre o fio 1 será:

• Fio 2:

Sobre o fio 2, em qualquer ponto, os vetores e são antiparalelos.



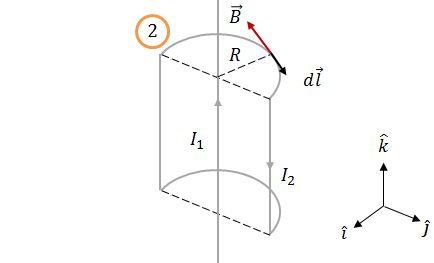
Logo:

• Fio 3:



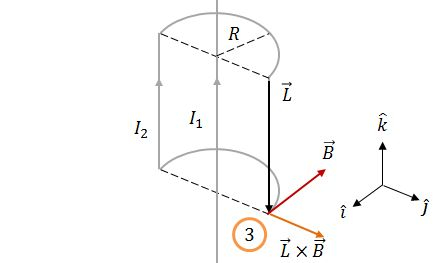
Assim, a força magnética sobre o fio 3 será:

• Fio 4:

No fio 4, em qualquer ponto, os vetores e são paralelos.

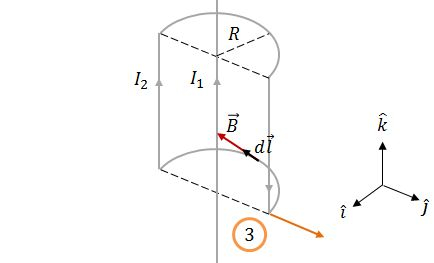
Logo:

Finalmente, a força magnética sobre a espira será:

Se a corrente variar com o tempo, haverá induzida na espira? Justifique.

Para que haja induzida, é necessário, de acordo com a Lei de Faraday, que haja uma variação do fluxo magnético sobre a espira.

O campo magnético, gerado pelo fio, em quaisquer dois pontos simétricos possuem o mesmo módulo, a mesma direção, mas sentidos contrários.

Isso significa que o fluxo total sobre a espira é nulo.

Assim, mesmo que a corrente varie, o fluxo magnético total sobre a espira continuará sendo nulo. Portanto, não haverá induzida.