A superfície matemática fechada no formato de um cubo de lado mostrada na figura está numa região do espaço onde existe um campo elétrico . Use as equações de Maxwell apropriadas para resolver os itens abaixo.
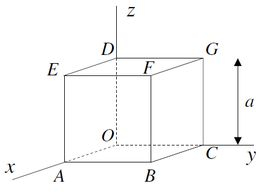
(a) (1,0 ponto) Calcule o fluxo do campo elétrico através das faces do cubo. Quanta carga existe dentro do cubo?
(b) (0,5 ponto) Calcule a densidade de carga dentro do cubo.
(c) (1,0 ponto) Na região em que se encontra o cubo pode existir um campo magnético , onde é uma constante? Justifique.
Passo 1
O fluxo do campo elétrico é dado por:
As faces laterais do cubo não contribuem para o cálculo do fluxo, já que nestas o campo elétrico é ortogonal ao vetor normal e, portanto, .
Passo 2
Na face inferior, , e, portanto, . Ou seja, esta face também não contribui para o cálculo do fluxo.
Passo 3
Nos resta apenas a face superior para calcular o fluxo. Temos, então:
Passo 4
Até agora, calculamos o fluxo elétrico dentro do cubo. Para calcular a carga interna, utilizamos a primeira equação de Maxwell, que nada mais é do que a lei de Gauss para o campo elétrico:
Usando a equação acima, chegamos em:
Passo 5
Para o item (b), utilizamos a lei de Gauss na sua forma diferencial, ou seja:
Assim sendo, calculamos a densidade de carga como:
Já que possui apenas a componente , . Logo,
Passo 6
Para o item (c), vamos olhar para a forma diferencial da lei de Gauss para o campo magnético:
Temos:
.
Ou seja, .
Portanto, um campo magnético da forma não poderia existir na região em que se encontra o cubo, pois este violaria a lei de Gauss.
Resposta
(a) O fluxo do campo elétrico através das faces do cubo é dado por:
A carga existente dentro do cubo é dada por:
(b) A densidade de carga dentro do cubo é dada por:
(c) Um campo magnético da forma não poderia existir na região em que se encontra o cubo, pois este violaria a lei de Gauss.