Três espiras circulares oscilam na presença de um campo magnético uniforme, como ilustrado na figura.
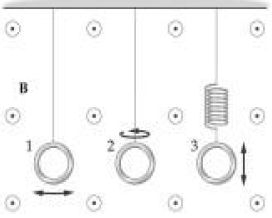
A espira 1 oscila de um lado para outro como um pêndulo, a espira 2 oscila em torno do seu eixo vertical e a espira 3 (presa na extremidade de uma mola) oscila para cima e para baixo.
Em todos os casos, as espiras se movimentam completamente dentro da região de campo magnético. Em quais espiras haverá uma fem induzida?
Apenas na espira 1
Espiras 1 e 2
Apenas na espira 3
Apenas na espira 2
Espiras 1, 2 e 3
Passo 1
De acordo com a Lei de Faraday, a fem induzida irá aparecer sempre que houver uma variação do fluxo magnético, logo:
Onde o fluxo magnético é dado por:
Nesse caso, como o campo magnético é uniforme e a área da espira é constante, podemos escrever o fluxo magnético como:
Onde é o ângulo formado pelos vetores e .
Sendo assim, para que haja fem induzida basta que um desses três termos varie, certo?
Passo 2
Em todos os casos, conforme já havíamos falado, o campo magnético é uniforme e a área da espira é constante. Assim, para que haja uma fem induzida, é necessária uma variação do ângulo .
Olhando as opções, nos casos 1 e 3 o ângulo permanece constante, de forma que não há fem induzida nesses casos. Já no caso 2, conforme a espira gira, o ângulo se altera, gerando uma fem induzida.
A resposta certa, portanto, é a letra .
Resposta
Apenas na espira 2