Exercícios Resolvidos de Manipulando ponteiros: ponteiros duplos, aritmética e vetores

Enunciado

Observe a seguinte expressão de aritmética de ponteiros. Qual o resultado?

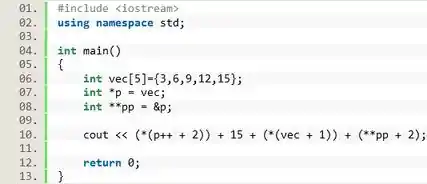
Passo 1

Vamos lá pessoal.

Basicamente, a questão quer que a gente analise a expressão da linha 10. Essa é uma expressão envolvendo ponteiros, ponteiros duplos e vetores. Então vamos tomar cuidado para não cometer nenhum erro.

Antes de começar, vamos dar uma revisada nas regras de precedência:

Note que os operadores de ponteiro e tem precedência bem alta. E vamos tomar cuidado para não confundir um operador de ponteiro com uma multiplicação.

Passo 2

Agora vamos pensar em pra onde cada ponteiro está apontando.

Sempre que a gente encontrar o vetor sem os colchetes podemos considera-lo como um ponteiro para .

Já é um ponteiro para a primeira posição do vetor. Ou seja, o ponteiro aponta para .

Por fim, o ponteiro é um ponteiro duplo que aponta para o ponteiro .

Passo 3

Com tudo estabelecido, vamos resolver a expressão. Pra começar vamos escrever a expressão e analisa-la.

Vamos olhar primeiro pras expressões dentro dos parêntesis destacados abaixo:

Tanto quanto são ponteiros para a primeira posição do vetor. Na expressão laranja o ponteiro é incrementado com o operador passa a apontar para a segunda posição do vetor, em seguida é somado , o resultado aponta para a quarta posição do vetor. A expressão é uma referência à . O operador acessa o valor contido neste endereço que é igual à

Na expressão em vermelho, é um ponteiro para a primeira posição do vetor. Ao adicionar somos enviados para a próxima posição. é uma referência a segunda posição do vetor. O operador acessa o valor contido neste endereço que é igual à

Por sua vez, é um ponteiro duplo que aponta para , que aponta para . Quando utilizamos dois operadores de desreferência em nós recebemos o valor contido em como resposta. Ou seja: , então a expressão em azul é:

Assim, a expressão é reduzida à:

Efetuando as somas temos:

Passo 4

Para garantir que nossa resposta está correta vamos executar o programa:

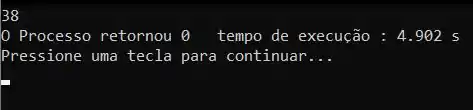
O que mostra que chegamos na resposta correta.