Cargas Axiais Distribuídas e Peso Próprio
Produzido por Pablo RicardoTeoria
![]()
Atenção: Não são todos os professores que ensinam e cobram esse assunto.
Se o seu professor já falou sobre “peso próprio” em sala de aula ou se ele já usou a fórmula...
...ou alguma outra fórmula parecida para resolver um exercício, então pode valer a pena estudar esse tópico.
;}
Introdução
Vamos dizer que a gente tem a coluna de aço abaixo, e que a gente ainda não colocou nenhuma carga nela:

Nessa situação, imaginamos que, como não existe nenhuma carga na coluna, a tensão normal nela vai ser nula.
Mas a verdade é que nós estamos desprezando o peso da coluna.
Na maioria dos exercícios, nós desprezamos mesmo o peso próprio das peças! Mas em alguns, vamos ter que considerar esse efeito.
Nesses casos, o que é que a gente faz?
Como é que a gente calcula a tensão normal ou a variação de comprimento devido ao peso próprio em uma peça?
![]()
Peso Próprio
Para responder essa pergunta, a primeira coisa que precisamos fazer é entender como que a força peso atua em uma peça.
Olhando para a nossa coluna, vamos imaginar que ela tem uma área de seção transversal e um comprimento :
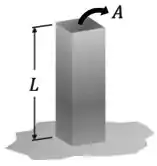
Nesse caso, ela vai ter um volume .
Dessa forma, se ela tiver uma densidade , ela vai ter uma massa .
E se a gravidade no local for , então a força peso total atuando na coluna vai ser:
Às vezes, vamos poder considerar que essa força atua bem no centro da coluna:
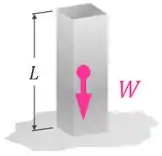
Mas a verdade é que a força peso não atua na coluna como essa carga axial pontual, única e total .
Na realidade, a força peso atua na coluna como uma carga axial distribuída :
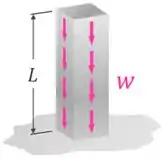
Agora lembra aí! 💡
Uma força distribuída é uma força que, ao invés de ser dada em (newtons), é dada em (newtons por metro) ou outra unidade de força/comprimento.
Daí que se a força peso pontual é , a força peso distribuída vai ser:
É bom guardar essa fórmula pois através dela nós percebemos como a distribuição de peso depende da área da seção transversal da peça.
Para a nossa coluna que tem uma área de seção transversal que não varia, a distribuição é uniforme ao longo de todo o comprimento da coluna.
Mas uma pirâmide, por exemplo, tem uma área de seção transversal que varia. Então a distribuição de peso também vai variar:
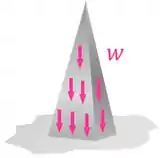
Cálculo de Tensões
Para calcular a tensão normal na nossa coluna, vamos fazer o que sempre fizemos para determinar as tensões em uma peça.
A única diferença é ter que trabalhar com uma força distribuída .
1º Passo – Diagrama de Corpo Livre
Vamos dizer que a nossa coluna tem um comprimento e que o peso próprio dela gera nela uma força uniformemente distribuída .
Além desse peso próprio, a coluna também é apoiada por uma reação realizada pelo chão, então o seu DCL (diagrama de corpo livre) fica assim:
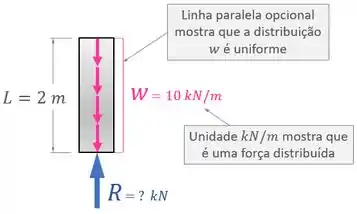
Queremos estar preparados para trabalhar com qualquer carga distribuída, então vamos também estudar um segundo exemplo:
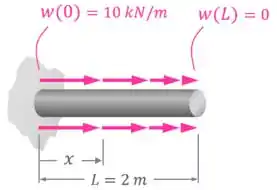
Nesse exemplo, é aplicada na barra uma força distribuída que varia linearmente desde no ponto até no ponto .
Para esse segundo exemplo, o DCL fica assim:
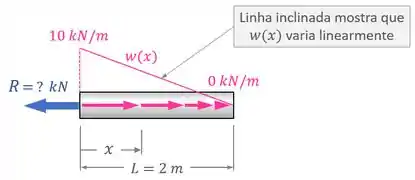
2º Passo – Equações de Equilíbrio
Feitos os DCLs, podemos aplicar o equilíbrio de forças nas peças para encontrar o valor das reações desconhecidas.
Mas para fazer isso, precisamos saber quantos de força as nossas cargas distribuídas vão gerar.
Então vamos pensar...
Se a carga na nossa coluna é uniforme (constante) ao longo de todo o comprimento da coluna, então é de se esperar que ela vai gerar:
Dessa forma, aplicando o equilíbrio de forças na nossa coluna, vamos encontrar que .
Agora...
Se a carga distribuída não for constante, como é o caso da carga variável na barra do nosso segundo exemplo, aí vamos ter que usar um truque. 🕵
O truque é: A força equivalente de uma força distribuída é igual à área do gráfico da força.
Como assim? 🤔
Então, sabe aquela linha inclinada que desenhamos para ? Olha para a área debaixo dela:
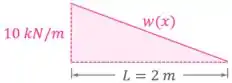
Aparece um triângulo de base e altura ! Calculando a área desse triângulo, temos:
Ou seja, a carga distribuída gera, ao total, de força.
Dessa forma, aplicando o equilíbrio de forças na barra, vamos encontrar .
E, por fim...
Ainda existe mais um truque: se a sua distribuição for muito louca e difícil de calcular a área, você ainda pode encontrar a força equivalente a ela usando a integral:
3º Passo – Análise dos Esforços Internos
Hora de encontrar as forças internas normais nas peças!
Aqui o esquema é:
- Secionar a peça em uma seção genérica de posição ; (Ou , ou , você escolhe a coordenada!)
- E dizer que a força normal é uma função de , ou seja, chamar ela de .
Para os nossos exemplos da coluna e da barra, essa análise fica assim:
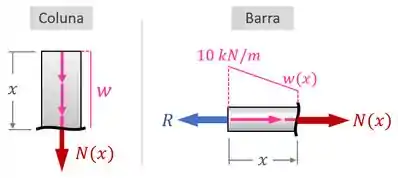
Aplicando o equilíbrio de forças e usando o truque da área nesses desenhos, conseguimos encontrar a força normal em cada peça.
4º Passo – Cálculo das Tensões
Encontrada a força normal na sua peça, tudo o que resta é aplicar a fórmula da tensão normal média .
Como a tensão e a força normal vão ser funções da posição , essa fórmula fica assim:
E, caso a área da sua peça também varie, você pode deixar essa fórmula assim:
Fórmula da Variação de Comprimento
E se um exercício pedir para que você calcule a variação de comprimento em uma peça com peso próprio (ou outra carga distribuída)?
Então... Nesses casos, existe uma fórmula específica para encontrar .
Olha só...
Primeiro, temos que a variação de comprimento é normalmente dada pela fórmula:
Por outro lado, em peças com diferentes segmentos onde os valores de , , e variam pontualmente, a variação de comprimento é dada pela somatório:
Mas em casos:
- De força normal variável, como qualquer caso de carga distribuída;
- E/ou de área variável, como o exemplo da pirâmide que vimos lá em cima;
- E/ou de módulo de elasticidade variável,
...essa fórmula de somatório, feita para mudanças pontuais de , e , não vai dar pro gasto.
Nesses casos, recorremos à evolução do somatório. ⚔
Fazemos um somatório de segmentos tão pequenos, com comprimentos tão pequenos, que o somatório deixa de ser um somatório e vira a integral:
Caso seu módulo de elasticidade e a sua área de seção transversal sejam constantes, você pode tirar esses valores para fora da integral, encontrando que: