Distribuição e Concentração de Tensões
Produzido por Pablo RicardoTeoria
Dica do Expert: Nessa teoria vamos aprender sobre o Princípio de Saint-Venant e sobre Concentradores de Tensões.
Em muitas universidades, esses assuntos só são vistos nas disciplinas ou da cadeia de resistência dos materiais.
Então se esses assuntos não fizerem parte do seu curso (ou do que vai cair na sua prova), sinta-se livre para pular esse tópico! 👍
Introdução
Vamos imaginar que a gente tem uma barra que está sob compressão por forças concentradas:

Se a gente quiser calcular a tensão normal nessa barra, só precisamos:
- Determinar a força interna normal nela;
- E, em seguida, aplicar a fórmula da tensão normal média .
Fazendo isso, conseguimos definir a tensão normal em uma seção qualquer da barra:

Mas existe um problema nesse análise que a gente fez.
Ela assume uma distribuição uniforme da tensão . Sendo que, muitas vezes, a distribuição de tensões em uma peça não é uniforme.
Então...
Como é a distribuição real de tensões em uma peça?
E quando é que é seguro considerar uma distribuição uniforme e usar a fórmula ?
E como é que a gente faz quando não for seguro?
Distribuição de Tensões e o Princípio de Saint-Venant
Para começar a responder essas perguntas, vamos continuar usando o exemplo da barra:

Essas forças atuam concentradas em um ponto da barra.
Então dá pra imaginar que, em uma seção bem próxima de uma dessas forças, ainda não “houve espaço” dentro da barra para que a força fosse espalhada.
Dessa forma, a tensão nessa seção vai ser concentrada em volta do ponto em que a força foi aplicada:
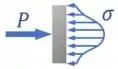
A medida que a gente se distancia da força , essa concentração vai diminuindo e a distribuição da tensão vai ficando cada vez mais uniforme:
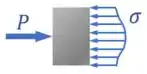
Agora, com a exceção de algumas situações avançadas, a gente não precisa se preocupar com essa distribuição não-uniforme de .
Isso porque existe o Princípio de Saint-Venant.
De acordo com ele, desde que a gente esteja suficientemente longe do ponto em que a força atua, podemos considerar que a distribuição de vai ser aproximadamente uniforme:
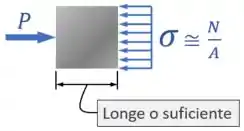
E assim, sendo a distribuição de aproximadamente uniforme, nós estamos livres para usar a fórmula da tensão normal média .
Concentradores de Tensão
Uma situação em que pode não ser seguro simplesmente usar a fórmula da tensão normal média é quando existem concentradores de tensões.
Concentradores de tensões acontecem sempre que a área da seção transversal de uma peça mudar de repente.
Então se a gente tiver uma placa de espessura e largura com um furo de diâmetro sendo tracionada...
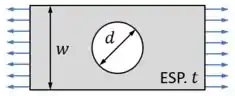
Esse furo vai ser um concentrador de tensões, já que, por causa dele, a área da seção transversal da placa vai mudar rapidamente de para :
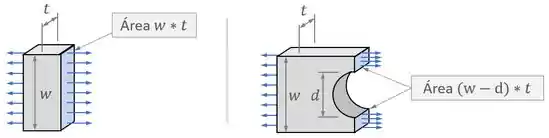
Outro concentrador de tensões vai ser quando a gente tiver uma placa, de espessura por exemplo, que muda de repende sua largura de uma largura maior para uma menor :
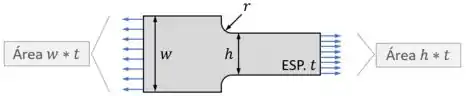
Nessas situações, muitas vezes é adicionado o adoçamento de raio mostrado na figura para diminuir um pouco da concentração de tensões.
Tensões Máximas
Agora, o que faz um concentrador de tensões ser especial é o fato de que as tensões máximas que vão ocorrer nele não são simplesmente a maior tensão normal média na peça.
Para as nossas placas com furo e redução na largura, por exemplo, a maior tensão normal média nessas peças vai ser:
Onde é a força interna normal e é a menor área na peça, de tal forma que:
- , para a placa com furo;
- & , para a placa com redução na largura.
Mas aí foram descobertas regiões perto dos furos (e das reduções de largura) em que as tensões eram ainda maiores que a tensão esperada:
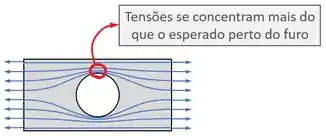
Por causa desse efeito, a tensão máxima nessas regiões (e na peça como um todo) é igual á tensão vezes um coeficiente :
Coeficiente de Concentração de Tensão
Esse coefiente é chamado de coeficiente de concentração de tensão.
Ele deve ser encontrado através do uso de gráficos como o do exemplo abaixo, feito para uma placa com furo:
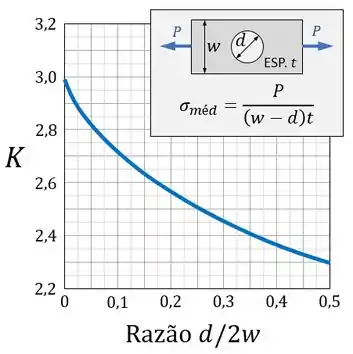
Ao usar um gráfico desses, a primeira coisa a ser feita é observar as dimensões indicadas no desenhozinho da peça.
Identificando o valor dessas dimensões na sua peça, você consegue calcular a razão indicada no eixo horizontal.
Finalmente, inserindo o valor calculado para a razão no gráfico, você consegue usar a curva do gráfico para encontrar o coeficiente correspondente.
Uma Observação Final
Dependendo do tipo de concentrador de tensões, o gráfico do coeficiente pode pedir que você calcule duas razões:
- Uma para definir a curva do gráfico que você vai usar;
- E outra para usar como entrada no eixo horizontal.
Um exemplo disso é o gráfico para o coeficiente em uma placa com redução de largura:
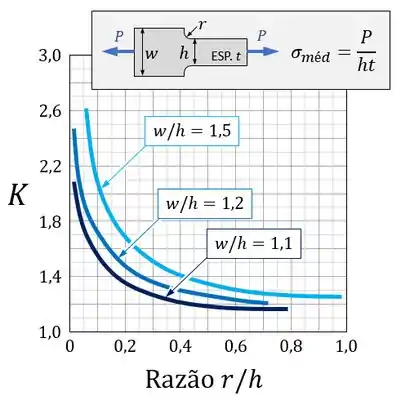
Nesse exemplo, você tem que:
- Calcular a razão entre as larguras para definir que curva você vai usar;
- E, em seguida, calcular a razão para encontrar o valor correspondente de .