Deformações em estruturas com inércia variando aleatoriamente (Regra de Simpson)
Produzido por Pablo RicardoTeoria
Introdução
Imagine um problema em que a inércia da nossa estrutura varie aleatoriamente, e por todo o comprimento da nossa estrutura. Como no exemplo que temos aqui em baixo:
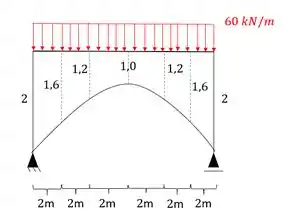
Regra de Simpson na estrutura isostática
Perceba que vamos começar por uma estrutura isostática para ficar fácil calcular a nossa fórmula.
E para isso suponha que o enunciado seja: Determine a rotação a elástica no apoio da esquerda sabendo que a seção possui base de 40 cm e altura variando conforme a figura acima. Use o modulo de elasticidade igual .
Para sabermos como e o que calcular precisamos da nossa fórmula, e nesse caso a fórmula que Simpson pensou foi a seguinte:
Em que é o momento de inércia de referencia e é o momento de inércia para cada seção:
Podemos simplificar essa fórmula chamando toda a parte interna da integral de , sendo assim teremos que:
Podemos então simplificar a nossa integral como:
E o que Simpson fez foi facilitar a nossa vida com a seguinte solução para a integral:
Em que precisamos primeiro saber que obrigatoriamente precisamos dividir a nossa estrutura em um número par de intervalos, em que o tamanho dos intervalos definimos como . Também precisamos saber que iremos numerar as seções começando pela seção mais extrema (que chamaremos de 0) indo até a seção da outra extremidade. Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente . Todas as seções pares com e todas as extremas com .
Resolvendo o exemplo
Ou seja, no nosso exemplo teremos que.
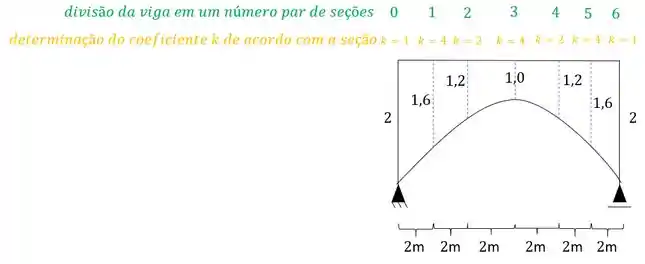
Também definimos no nosso exemplo que o valor de é de 2m, além do mais dividimos a nossa estrutura em 6 seções (um número par de seções) com tamanhos iguais.
Agora só falta determinarmos o valor de: , e .
Sabemos que nada mais é que uma simplificação da seguinte conta:
Em que:
Determinando os diagramas
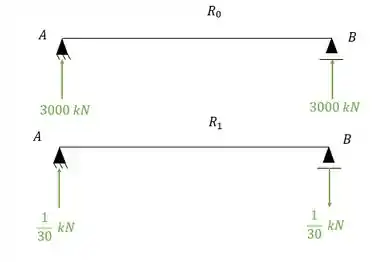
No nosso exemplo isostático queremos saber a rotação no apoio esquerdo, sendo assim podemos dizer que:
- Diagrama de momentos fletores para o carregamento externo para cada uma das seções
- Diagrama de momentos fletores devido a carga unitária no ponto e na direção que queremos saber o deslocamento, que nesse caso é rotação:
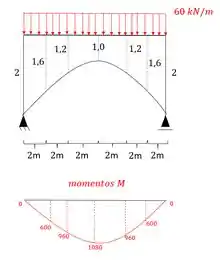
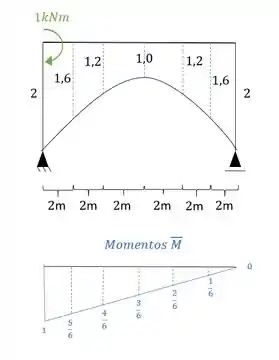
E agora por fim só precisamos relacionar os e .
Se para o calculo de podemos fazer:
Se substituirmos na fórmula teremos que:
E como vimos, costumamos usar a menor seção como referência, sendo assim sabemos que:
Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente.
No fim basta fazer:
E assim determinar as deformações no nosso sistema. No nosso exemplo teremos que:
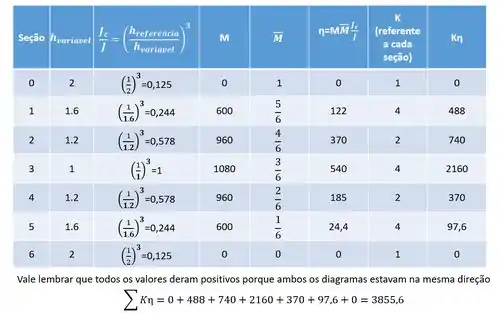
Substituindo na fórmula teremos que:
Estrutura hiperestática
Na estrutura hiperestática precisamos lembrar da nossa formulazinha, ou seja, se por exemplo, tivermos apenas um hiperestático, devemos fazer a seguinte equação:
Já tendo o nosso conhecimento da regra de Simpson, vamos dar uma modificada na nossa tabela, mas o princípio permanece igual:

Em que:
Lembrando que o sistema isostático aqui é o sistema obtido a partir da quebra dos vínculos hiperestáticos do sistema principal hiperestático.
Se substituirmos na nossa fórmula teremos que:
E como já sabemos, tendo o valor de obtemos qualquer esforço na nossa estrutura pelas relações.
Resolvendo o exemplo
Determinando os diagramas
Estrutura hiperestática
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
Determine o deslocamento vertical do ponto C da viga dada abaixo;
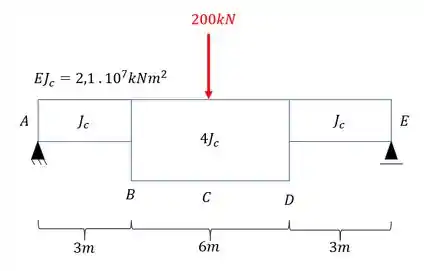
Passo 1
A primeira coisa que devemos notar é que nossa estrutura é uma estrutura isostática, logo, não precisaremos quebrar nenhum vínculo para determinação de hiperestáticos:
A segunda coisa que devemos fazer é dividir a nossa seção em uma quantidade para de seções, pois lembre-se que para usarmos essa fórmula:
Precisamos de uma quantidade par de seções, e que podemos determinar os coeficientes das seções seguindo a seguinte regra:
Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente . Todas as seções pares com e todas as extremas com .
Sendo assim teremos que:
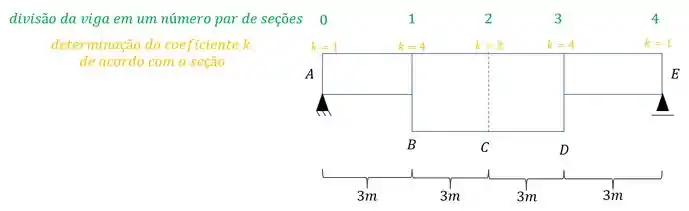
Também definimos no nosso exemplo que o valor de é de 3m, além do mais dividimos a nossa estrutura em 4 seções (um número par de seções) com tamanhos iguais.
Agora só falta determinarmos o valor de: , e .
Sabemos que nada mais é que uma simplificação da seguinte conta:
Em que:
Passo 2
No nosso exemplo isostático queremos saber o deslocamento vertical do ponto C no meio da viga, sendo assim podemos dizer que:
- Diagrama de momentos fletores para o carregamento externo para cada uma das seções será
- Diagrama de momentos fletores devido a carga unitária no ponto e na direção que queremos saber o deslocamento, que nesse caso é deslocamento vertical:
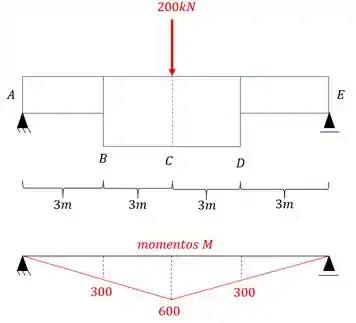
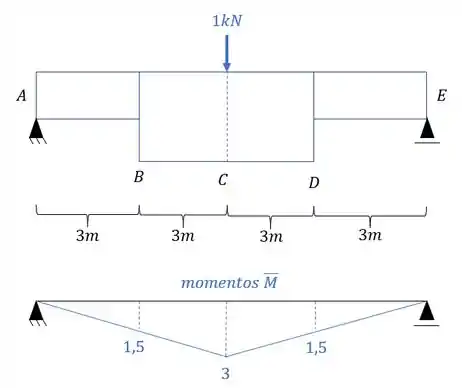
E agora por fim só precisamos relacionar os e .
No caos temos para nossa seção duas possibilidades, que seria o caso de e , e nesse caso usaremos como referência o menor.
Se substituirmos na fórmula teremos que:
Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente.
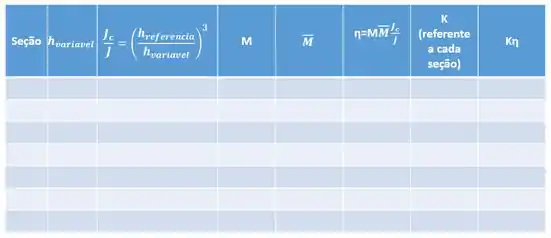
No fim basta fazer:
E assim determinar as deformações no nosso sistema. No nosso exemplo teremos que:
Perceba que nas seções 1 e 3, que são intermediarias, usamos a média entre as seções para determinar a inércia relativa entre as seções.
Substituindo na fórmula teremos que:
Resposta
Exercício Resolvido #2
Origem do Exercício
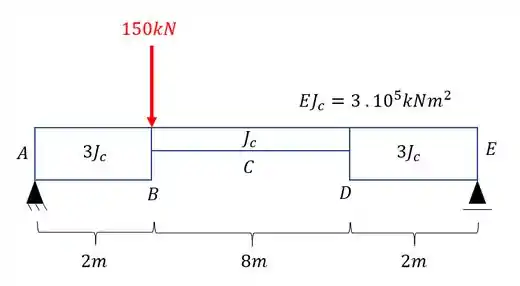
Determine o deslocamento vertical do ponto D da viga dada abaixo;
Passo 1
A primeira coisa que devemos notar é que nossa estrutura é uma estrutura isostática, logo, não precisaremos quebrar nenhum vínculo para determinação de hiperestáticos:
A segunda coisa que devemos fazer é dividir a nossa seção em uma quantidade par de seções, pois lembre-se que para usarmos essa fórmula:
Precisamos de uma quantidade par de seções, e que podemos determinar os coeficientes das seções seguindo a seguinte regra:
Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente . Todas as seções pares com e todas as extremas com .
Sendo assim teremos que:
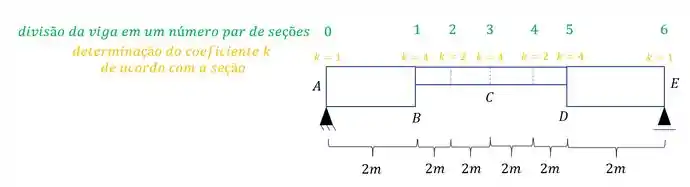
Também definimos no nosso exemplo que o valor de é de 2m, além do mais dividimos a nossa estrutura em 6 seções (um número par de seções) com tamanhos iguais.
Agora só falta determinarmos o valor de: , e .
Sabemos que nada mais é que uma simplificação da seguinte conta:
Em que:
Passo 2
No nosso exemplo isostático queremos saber o deslocamento vertical do ponto D, sendo assim podemos dizer que:
- Diagrama de momentos fletores para o carregamento externo para cada uma das seções será
- Diagrama de momentos fletores devido a carga unitária no ponto e na direção que queremos saber o deslocamento, que nesse caso é deslocamento vertical:
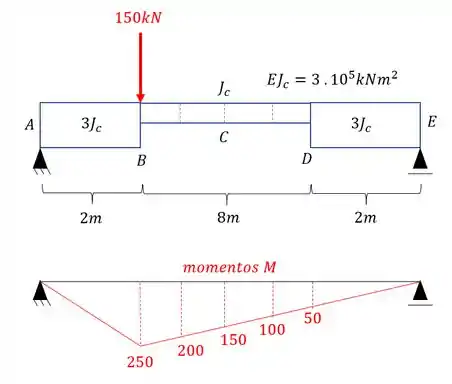
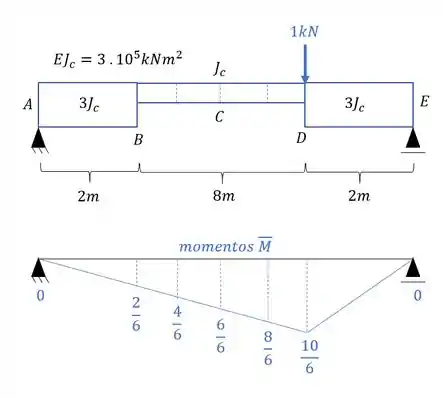
E agora por fim só precisamos relacionar os e .
No caos temos para nossa seção duas possibilidades, que seria o caso de e , e nesse caso usaremos como referência o menor.
Se substituirmos na fórmula teremos que:
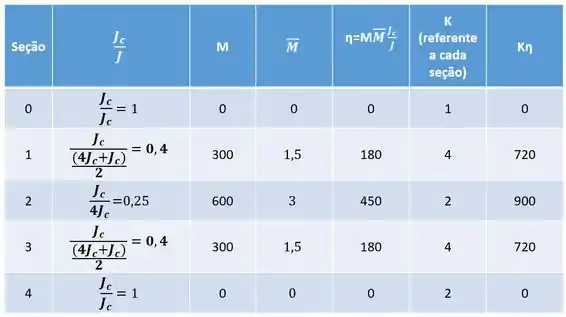
Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente.
No fim basta fazer:
E assim determinar as deformações no nosso sistema. No nosso exemplo teremos que:
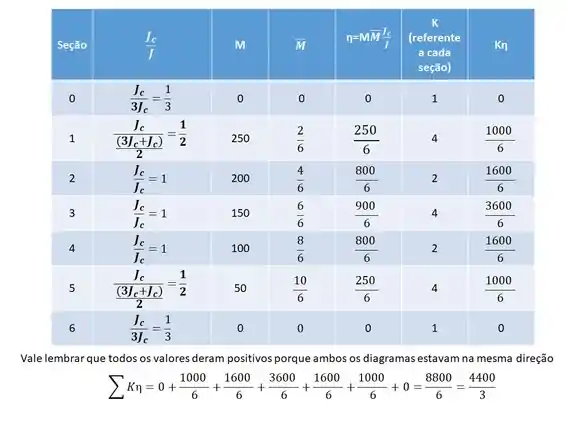
Perceba que nas seções 1 e 5, que são intermediarias, usamos a média entre as seções para determinar a inércia relativa entre as seções.
Substituindo na fórmula teremos que:
Resposta
Exercício Resolvido #3
Elaboração própria
Determine o deslocamento angular na extremidade da viga dada abaixo. Dado:
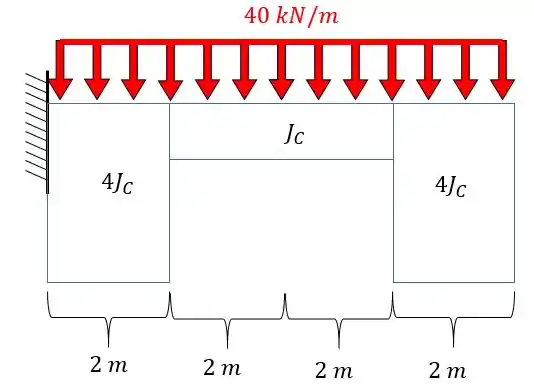
Passo 1
Temos aqui um problema em que há uma viga engastada sujeita a um carregamento uniforme de e essa viga tem inércia variável. O fato dela ter inércia variável que justifica a utilização do método de Simpson.
Para resolver esse problema a gente vai ter que utilizar a equação do método de Simpson:
Vamos vendo cada termo conforme formos resolvendo o problema, o mais importante é lembrar que devemos separar as seções, numerá-las e calcular a inércia relativa. Ao fim desse processo a gente aplica o momento de inércia e descobre o deslocamento, beleza? Então vamos seguir!
Passo 2
A primeira coisa que devemos notar é que nossa estrutura é uma estrutura isostática, logo, não precisaremos quebrar nenhum vínculo para determinação de hiperestáticos:
A segunda coisa que devemos fazer é dividir a nossa seção em uma quantidade para de seções, pois lembre-se que para usarmos essa fórmula:
Precisamos de uma quantidade par de seções, e que podemos determinar os coeficientes das seções seguindo a seguinte regra:
Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente . Todas as seções pares com e todas as extremas com .
Sendo assim teremos que:
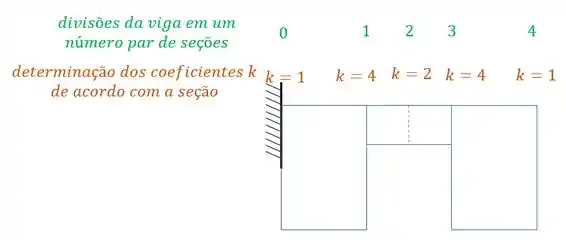
Também definimos no nosso exemplo que o valor , além do mais dividimos a nossa estrutura em 4 seções (um número par de seções) com tamanhos iguais.
Agora só falta determinarmos o valor de: , e .
Sabemos que nada mais é que uma simplificação da seguinte conta:
Em que:
Passo 3
No nosso exemplo isostático queremos saber o deslocamento angular da extremidade da viga, sendo assim podemos dizer que:
- Diagrama de momentos fletores para o carregamento externo para cada uma das seções será
- Diagrama de momentos fletores devido a carga unitária no ponto e na direção que queremos saber o deslocamento, que nesse caso é o deslocamento angular:
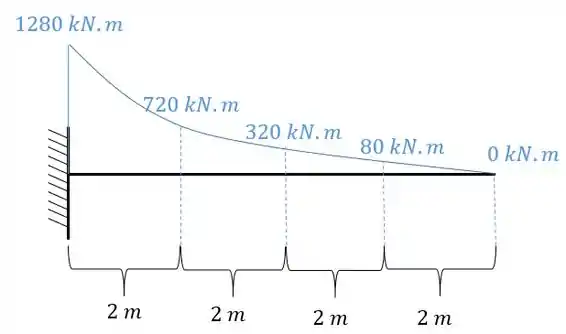
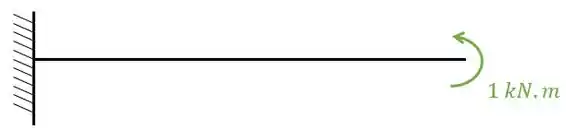
E agora por fim só precisamos relacionar os e .
No caso temos para nossa seção duas possibilidades, que seria o caso de e , e nesse caso usaremos como referência o menor.
Se substituirmos na fórmula teremos que:
Passo 4
Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente.
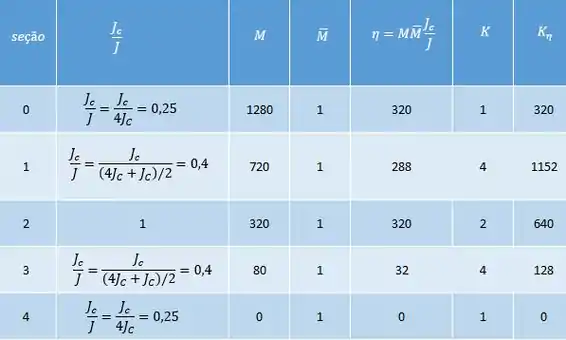
No fim basta fazer:
E assim determinar as deformações no nosso sistema.
Perceba que nas seções 1 e 3, que são intermediarias, usamos a média entre as seções para determinar a inércia relativa entre as seções.
Substituindo na fórmula teremos que:
Resposta
Exercício Resolvido #4
Origem do Exercício
Para a viga abaixo com inércia constante, determine o deslocamento vertical do ponto C usando a regra de Simpson;
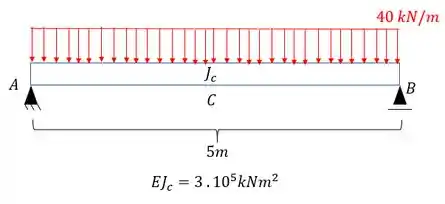
Passo 1
A primeira coisa que devemos notar é que nossa estrutura é uma estrutura isostática, logo, não precisaremos quebrar nenhum vínculo para determinação de hiperestáticos:
A segunda coisa que devemos fazer é dividir a nossa seção em uma quantidade par de seções, pois lembre-se que para usarmos essa fórmula:
Precisamos de uma quantidade par de seções, e que podemos determinar os coeficientes das seções seguindo a seguinte regra:
Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente . Todas as seções pares com e todas as extremas com .
Sendo assim, como a inércia é constante, vamos dividir em 10 seções afim de ficarmos o mais próximo possível do valor real, teremos assim que:
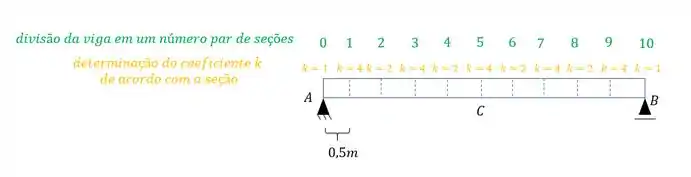
Também definimos no nosso exemplo que o valor de é de 0,5m, além do mais dividimos a nossa estrutura em 10 seções (um número par de seções) com tamanhos iguais.
Agora só falta determinarmos o valor de: , e .
Sabemos que nada mais é que uma simplificação da seguinte conta:
Em que:
Passo 2
No nosso exemplo isostático queremos saber o deslocamento vertical do ponto C, sendo assim podemos dizer que:
- Diagrama de momentos fletores para o carregamento externo para cada uma das seções será
- Diagrama de momentos fletores devido a carga unitária no ponto e na direção que queremos saber o deslocamento, que nesse caso é deslocamento vertical:
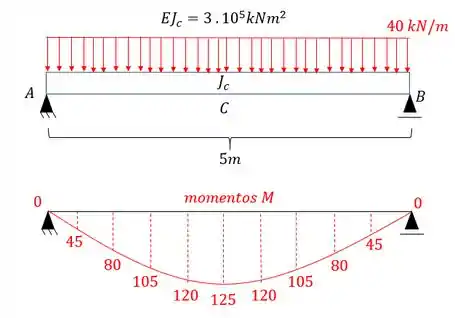
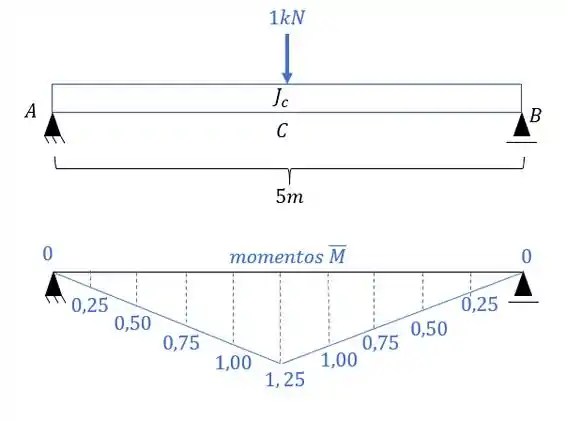
E agora por fim só precisamos relacionar os e .
no nosso caso a seção é constante, ou seja, a relação entre J será constante e igual a 1, sendo assim teremos que se substituirmos na fórmula teremos que:
Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente.
No fim basta fazer:
E assim determinar as deformações no nosso sistema. No nosso exemplo teremos que:
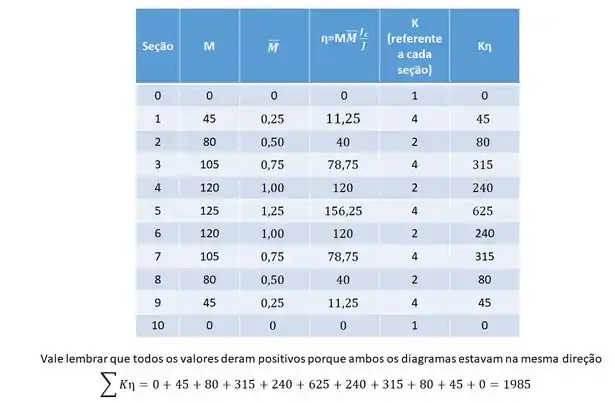
Substituindo na fórmula teremos que:
Resposta
Exercício Resolvido #5
Elaboração própria
Determine o deslocamento do ponto médio da viga abaixo. Dado
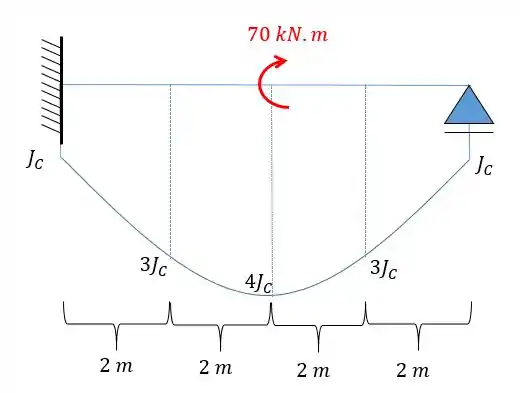
Passo 1
Temos aqui um problema em que há uma viga engastada sujeita a um momento de e essa viga tem inércia variável. O fato dela ter inércia variável que justifica a utilização do método de Simpson.
Para resolver esse problema a gente vai ter que utilizar a equação do método de Simpson:
Pode ficar tranquilo que vamos vendo cada termo conforme formos resolvendo o problema, o mais importante é lembrar que devemos separar as seções, numerá-las e calcular a inércia relativa. Ao fim desse processo a gente aplica o momento de inércia e descobre o deslocamento, beleza? Então vamos seguir!
Passo 2
A primeira coisa que devemos notar é que nossa estrutura é uma estrutura hiperestática, logo, precisaremos quebrar um vínculo para determinação de hiperestáticos. Vai ficar da seguinte forma:
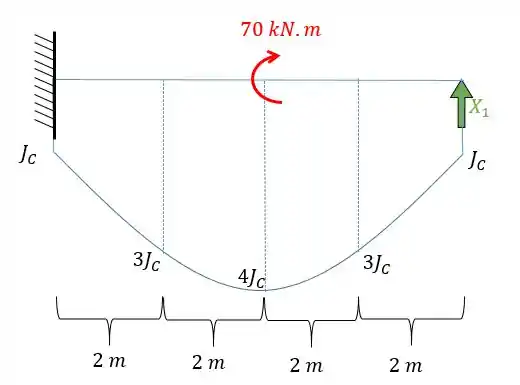
A segunda coisa que devemos fazer é dividir a nossa seção em uma quantidade para de seções, pois lembre-se que para usarmos essa fórmula:
Precisamos de uma quantidade par de seções, e que podemos determinar os coeficientes das seções seguindo a seguinte regra:
Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente . Todas as seções pares com e todas as extremas com .
Sendo assim teremos que:
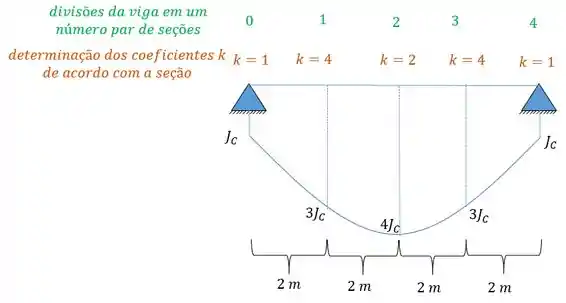
Também definimos no nosso exemplo que o valor , além do mais dividimos a nossa estrutura em 4 seções (um número par de seções) com tamanhos iguais.
Agora só falta determinarmos o valor de: , e .
Sabemos que nada mais é que uma simplificação da seguinte conta:
Em que:
Passo 3
No nosso exemplo queremos descobrir as reações de apoio, sendo assim podemos dizer que:
- Diagrama de momentos fletores para o carregamento externo para cada uma das seções será
- Diagrama de momentos fletores devido a carga unitária:
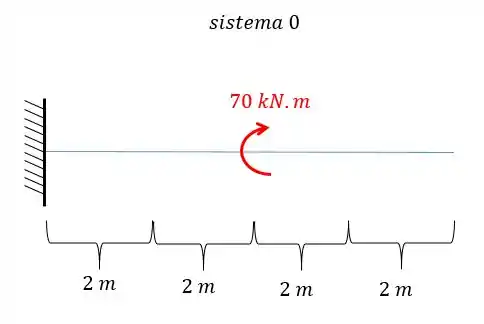
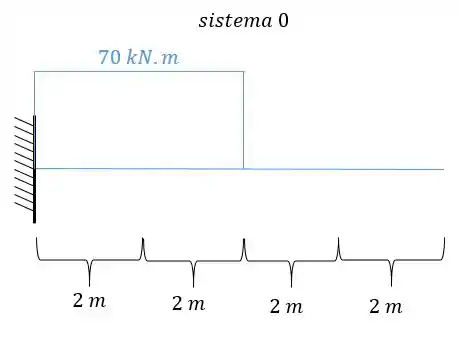
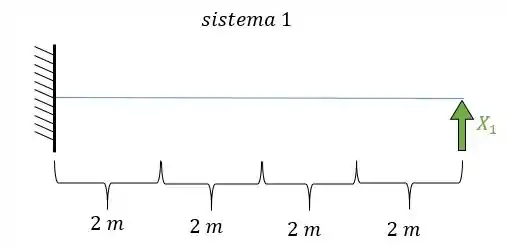
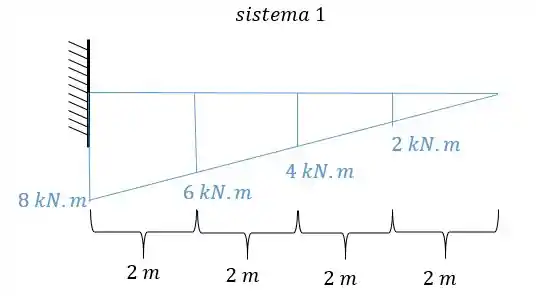
E agora por fim só precisamos relacionar os e .
Se substituirmos na fórmula teremos que:
Passo 4
Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente. Só que desta vez vamos fazer duas tabelas.
Começando pelo deslocamento :
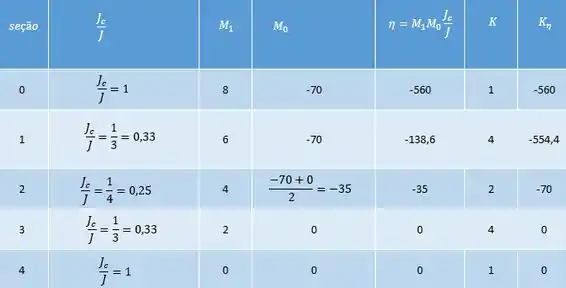
No fim basta fazer:
E assim determinar as deformações no nosso sistema.
Substituindo na fórmula teremos que:
Passo 5
Agora para o deslocamento .
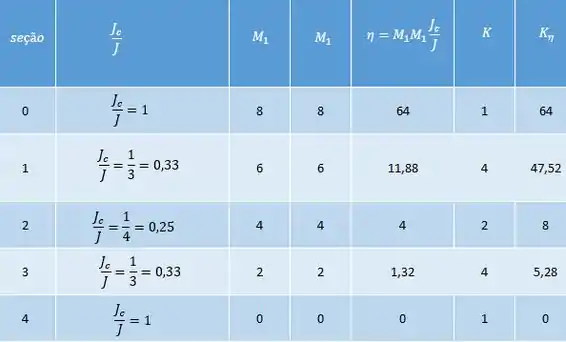
No fim basta fazer:
E assim determinar as deformações no nosso sistema.
Substituindo na fórmula teremos que:
Passo 6
Agora é só somar os resultados:
Resposta
Exercício Resolvido #6
Elaboração própria
Determine as reações de apoio da viga abaixo.
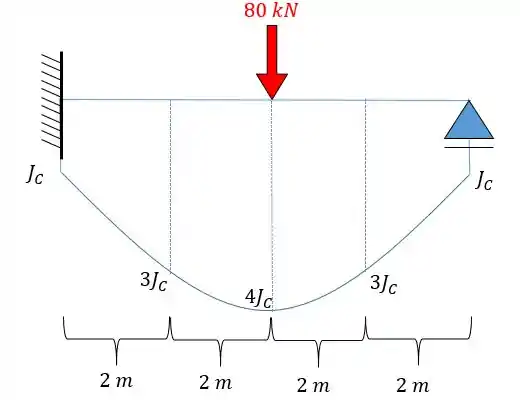
Passo 1
Temos aqui um problema em que há uma viga engastada sujeita a um carregamento de e essa viga tem inércia variável. O fato dela ter inércia variável que justifica a utilização do método de Simpson.
Para resolver esse problema a gente vai ter que utilizar a equação do método de Simpson:
Pode ficar tranquilo que vamos vendo cada termo conforme formos resolvendo o problema, o mais importante é lembrar que devemos separar as seções, numerá-las e calcular a inércia relativa. Ao fim desse processo a gente aplica o momento de inércia e descobre o deslocamento, beleza? Então vamos seguir!
Passo 2
A primeira coisa que devemos notar é que nossa estrutura é uma estrutura hiperestática, logo, precisaremos quebrar um vínculo para determinação de hiperestáticos. Vai ficar da seguinte forma:
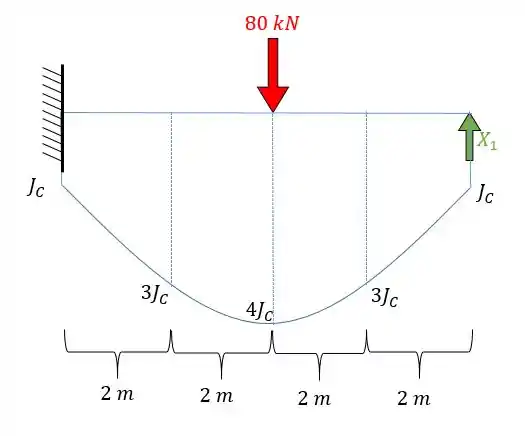
A segunda coisa que devemos fazer é dividir a nossa seção em uma quantidade para de seções, pois lembre-se que para usarmos essa fórmula:
Precisamos de uma quantidade par de seções, e que podemos determinar os coeficientes das seções seguindo a seguinte regra:
Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente . Todas as seções pares com e todas as extremas com .
Sendo assim teremos que:
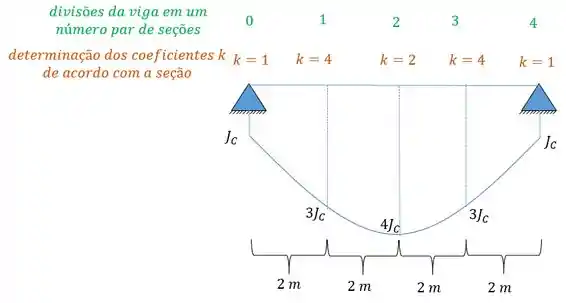
Também definimos no nosso exemplo que o valor , além do mais dividimos a nossa estrutura em 4 seções (um número par de seções) com tamanhos iguais.
Agora só falta determinarmos o valor de: , e .
Sabemos que nada mais é que uma simplificação da seguinte conta:
Em que:
Passo 3
No nosso exemplo queremos descobrir as reações de apoio, sendo assim podemos dizer que:
- Diagrama de momentos fletores para o carregamento externo para cada uma das seções será
- Diagrama de momentos fletores devido a carga unitária:
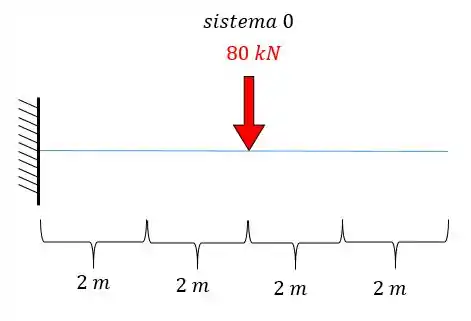
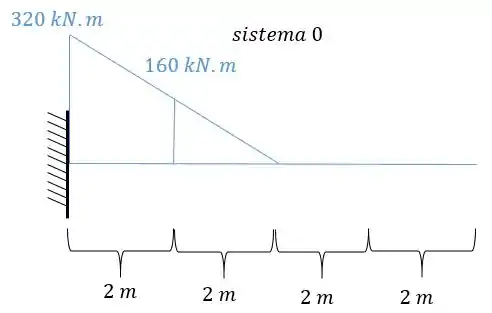
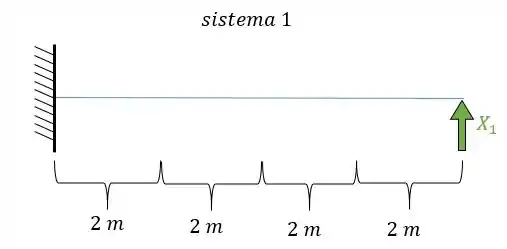
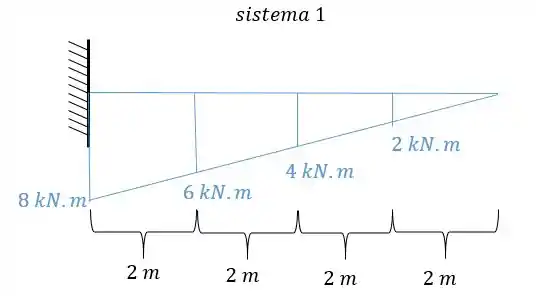
E agora por fim só precisamos relacionar os e .
Se substituirmos na fórmula teremos que:
Passo 4
Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente. Só que desta vez vamos fazer duas tabelas.
Começando pelo deslocamento :
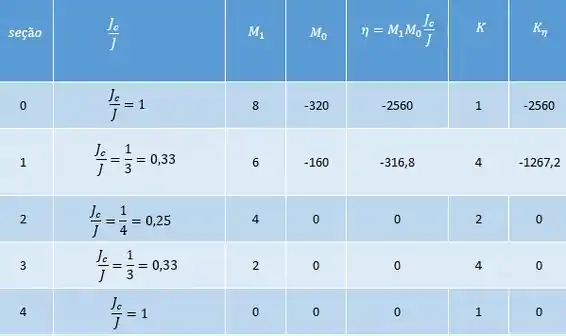
No fim basta fazer:
E assim determinar as deformações no nosso sistema.
Substituindo na fórmula teremos que:
Passo 5
Agora para o deslocamento .
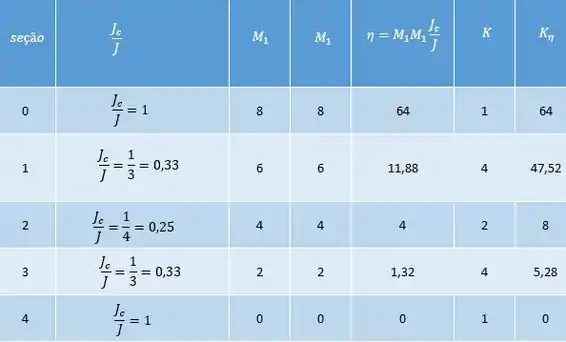
No fim basta fazer:
E assim determinar as deformações no nosso sistema.
Substituindo na fórmula teremos que:
Passo 6
Agora basta achar o valor do nosso hiperestático :
Substituindo:
Passo 7
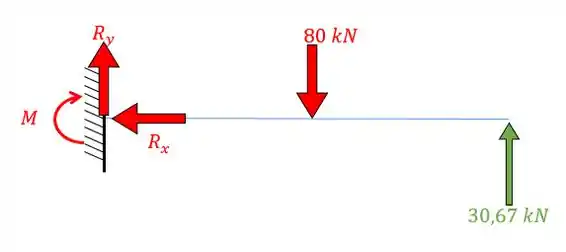
Encontrando o resto do sistema pelas equações de equilíbrio estático vamos ter:
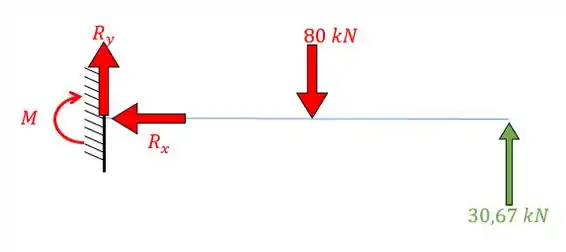
Resposta
Exercício Resolvido #7
Origem do Exercício
Para estrutura abaixo determine as reações de apoio e diagrama de momentos pela regra de Simpson:
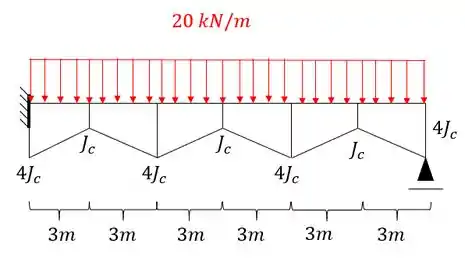
Passo 1
A primeira coisa que devemos notar é que nossa estrutura é uma estrutura hiperestática, logo, precisamos quebrar alguns vínculos para determinação de hiperestáticos:
A segunda coisa que devemos fazer é dividir a nossa seção em uma quantidade par de seções, pois lembre-se que para usarmos essa fórmula:
E como nossa estrutura é hiperestática a nossa fórmula terá dois termos dados pelo sistema:
Sendo assim teríamos que fazer:
Antes de qualquer coisa precisamos determinar o nosso número de hiperestáticos, para assim podermos quebrar vínculos e com isso podermos ter a nossa estrutura isostática a ser resolvida. Perceba que:
- Temos um apoio d terceiro gênero que nos dará 3 incógnitas
- Temos um apoio do primeiro gênero que nos dará mais 1 incógnita
- Totalizando 4 incógnitas
- Como não temos rótulas o número de equações será de 3
- Dessa forma teremos 4-3=1 hiperestático
Podemos quebrar o vinculo de momento do apoio a esquerda, e com isso a nossa estrutura passa a ser:
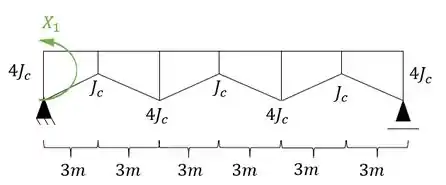
Passo 2
Agora precisamos de uma quantidade par de seções, e que podemos determinar os coeficientes das seções seguindo a seguinte regra:
Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente . Todas as seções pares com e todas as extremas com .
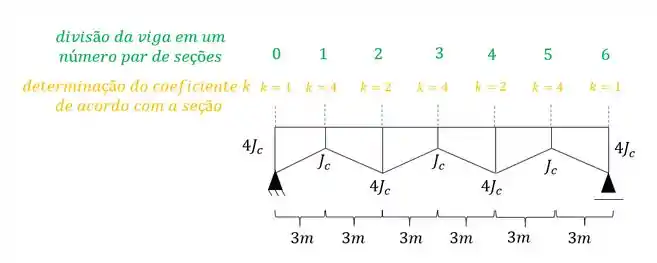
Também definimos no nosso exemplo que o valor de é de 3m, além do mais dividimos a nossa estrutura em 6 seções (um número par de seções) com tamanhos iguais.
Agora só falta determinarmos o valor de: , e .
Sabemos que nada mais é que uma simplificação da seguinte conta:
Em que:
Que para nosso caso sofrerá uma pequena mudança dada por:
Em que:
Passo 3
Como queremos saber as nossas reações de apoio, precisamos determinar a solução do nosso sistema, e para solucionarmos o nosso sistema, precisamos determinar os diagramas, sendo assim teremos que:
- Diagrama de momentos fletores para o carregamento externo para cada uma das seções será
- Diagrama de momentos fletores devido ao hiperestático com a carga unitária agindo na estrutura isostática, sendo assim teremos que:
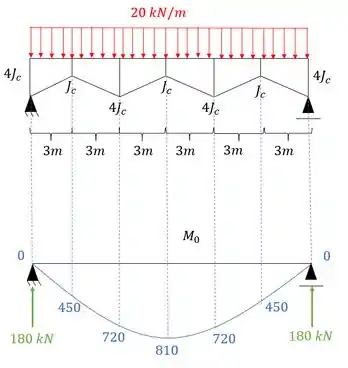
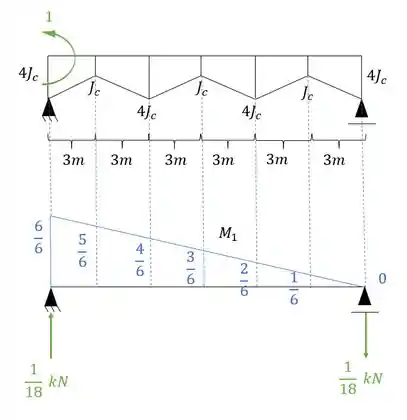
E agora por fim só precisamos relacionar os e .
No nosso caso temos 2 tipos de seções dadas por
E vamos usar como referência a menor inércia, ou seja, .
Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente.
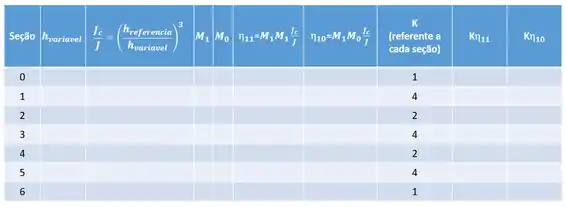
No fim basta fazer:
E assim determinar as deformações no nosso sistema. No nosso exemplo teremos que:
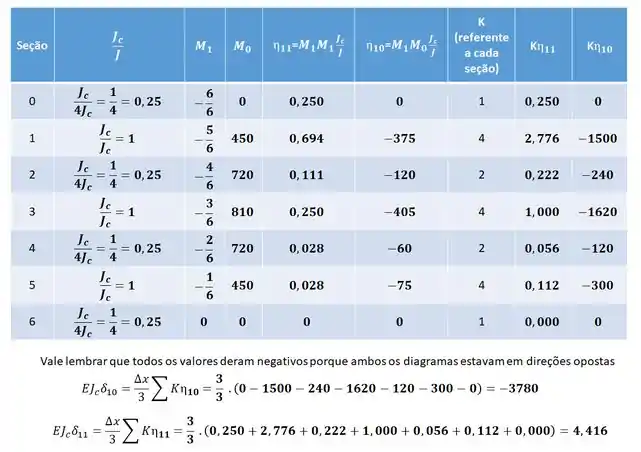
Substituindo na fórmula teremos que:
Ou seja, já descobrimos quanto vale o momento fletor da nossa reação de apoio. Para determinarmos o resto das reações devemos usar a fórmula:
Em que:
Separando os dois sistemas temos que;
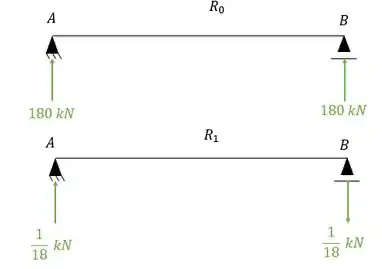
Para o diagrama de momentos faremos a mesma coisa:
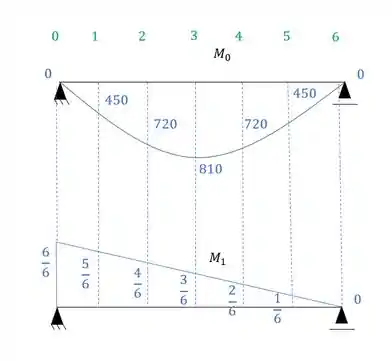
Logo o diagrama será dado por:
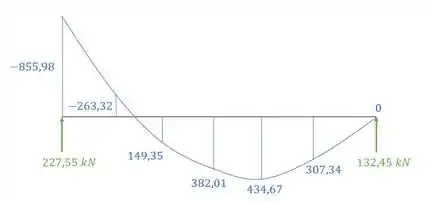
Resposta
Exercício Resolvido #8
Origem do Exercício
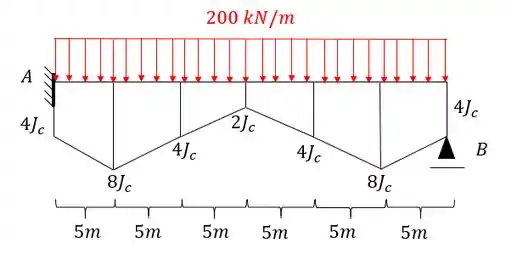
Para estrutura abaixo determine as reações de apoio e diagrama de momentos pela regra de Simpson:
Passo 1
A primeira coisa que devemos notar é que nossa estrutura é uma estrutura hiperestática, logo, precisamos quebrar alguns vínculos para determinação de hiperestáticos:
A segunda coisa que devemos fazer é dividir a nossa seção em uma quantidade par de seções, pois lembre-se que para usarmos essa fórmula:
E como nossa estrutura é hiperestática a nossa fórmula terá dois termos dados pelo sistema:
Sendo assim teríamos que fazer:
Antes de qualquer coisa precisamos determinar o nosso número de hiperestáticos, para assim podermos quebrar vínculos e com isso podermos ter a nossa estrutura isostática a ser resolvida. Perceba que:
- Temos um apoio do terceiro gênero que nos dará 3 incógnitas
- Temos um apoio do primeiro gênero que nos dará mais 1 incógnita
- Totalizando 4 incógnitas
- Como não temos rótulas o número de equações será de 3
- Dessa forma teremos 4-3=1 hiperestático
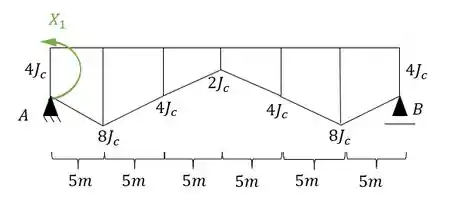
Podemos quebrar o vinculo de momento do apoio a esquerda, e com isso a nossa estrutura passa a ser:
Passo 2
Agora precisamos de uma quantidade par de seções, e que podemos determinar os coeficientes das seções seguindo a seguinte regra:
Todas as seções numeradas com valores impares, serão multiplicadas pelo coeficiente . Todas as seções pares com e todas as extremas com .
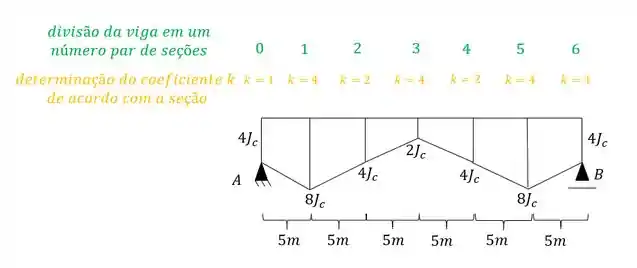
Também definimos no nosso exemplo que o valor de é de 5m, além do mais dividimos a nossa estrutura em 6 seções (um número par de seções) com tamanhos iguais.
Agora só falta determinarmos o valor de: , e .
Sabemos que nada mais é que uma simplificação da seguinte conta:
Em que:
Que para nosso caso sofrerá uma pequena mudança dada por:
Em que:
Passo 3
Como queremos saber as nossas reações de apoio, precisamos determinar a solução do nosso sistema, e para solucionarmos o nosso sistema, precisamos determinar os diagramas, sendo assim teremos que:
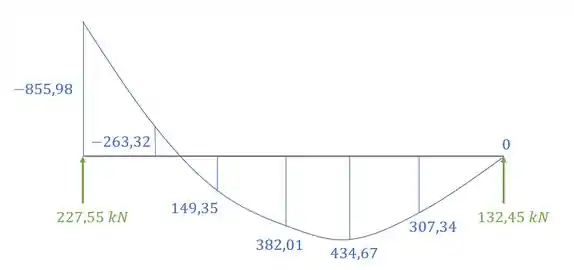
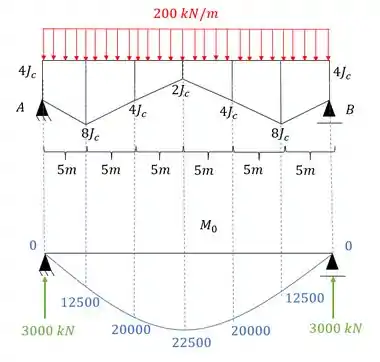
- Diagrama de momentos fletores para o carregamento externo para cada uma das seções será
- Diagrama de momentos fletores devido ao hiperestático com a carga unitária agindo na estrutura isostática, sendo assim teremos que:
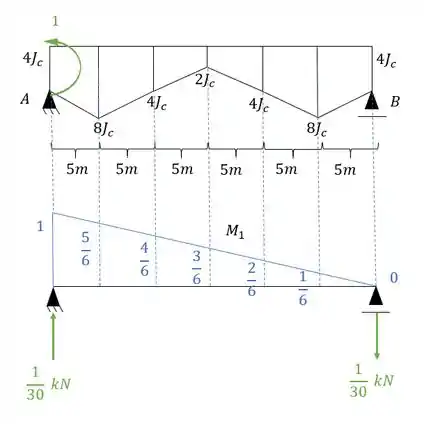
E agora por fim só precisamos relacionar os e .
No nosso caso temos 3 tipos de seções dadas por
E vamos usar como referência a menor inércia, ou seja, .
Como você pode ver, temos muitos valores para trabalhar, ao invés de fazer um a um de maneira desorganizada, podemos fazer essa tabelinha aqui pra ajudar a gente.
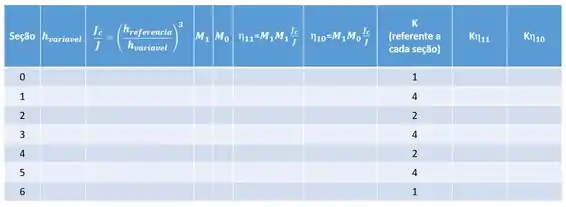
No fim basta fazer:
E assim determinar as deformações no nosso sistema. No nosso exemplo teremos que:
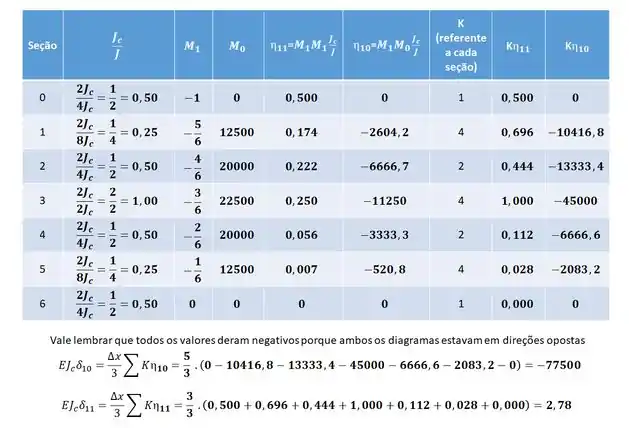
Substituindo na fórmula teremos que:
Ou seja, já descobrimos quanto vale o momento fletor da nossa reação de apoio. Para determinarmos o resto das reações devemos usar a fórmula:
Em que:
Separando os dois sistemas temos que;