Deslocabilidade Externa e Interna de uma Estrutura
Teoria
Introdução
Agora vamos entrar em uma nova maneira de determinar o número de incógnitas de um problema.
Pra começar as deslocabilidades são incógnitas de deformação que iremos determinar no nosso problema. Como assim? É isso que vamos ver usando o conceito de graus de liberdade.
Deslocabilidade interna
Vamos nos concentrar primeiro no número de deslocabilidades internas. Basicamente são o número de nós que temos na nossa estrutura, que avaliamos como nós que irão rotacionar, como assim? Vamos começar com uma viga que fica mais fácil de visualizar.
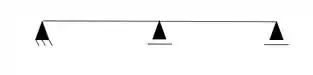
Perceba que cada apoio irá representar um nó, assim nomeando esses nós teremos que:
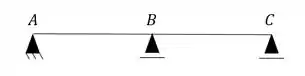
Agora como podemos usar o nosso conceito de graus de liberdade? Vamos ver nó por nó:
Nó A
Perceba que o nosso nó A é um apoio do segundo gênero, ou seja, impede o deslocamento vertical e o deslocamento horizontal. Ou seja, já sabemos que no nosso nó A não irá possui esses dois graus de liberdade, porém, perceba que ele pode rotacionar, ou seja, existem, no plano 3 graus de liberdade:
- Vertical
- Horizontal
- Rotação
Sabemos que desses o único que A pode fazer é o último, logo, ele possui 1 grau de liberdade que vou representar da seguinte maneira:
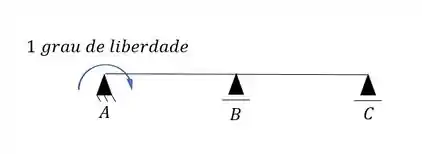
Nó B
Analisando o nó B, vemos que agora temos um apoio do primeiro gênero, ou seja, ele impede o movimento vertical, mas permite o horizontal e a rotação, certo?
Porém lembre-se que a analise iniciou pelo nó A, e já vimos que o nó A não permite movimento na horizontal, sendo assim, ele também irá travar o nó B.
Ou seja, o nó B também vai estar suscetível a efeito de rotação, e com isso teremos mais um grau de liberdade.
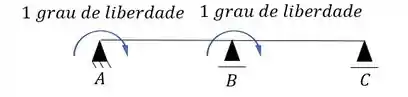
Ou seja, agora temos no total 2 graus de liberdade.
Nó C
O nó C, vai ser idêntico ao nó B, mas com o seguinte cuidado. Lembra que para o nó B sabíamos que ele poderia deslocar na horizontal, porém o no A trava ele? Ou seja, se o no B é travado, ele automaticamente trava o nó C. Qual o cuidado? O nó C não é travado pelo nó A, mas pelo nó B. isso pode parecer obvio por ser uma viga, mas em pórticos vamos ver que precisamos conhecer os nós próximos ao nó que estudamos, e não aos nós distantes. Sendo assim o nosso nó C tem apenas 1 graus de liberdade que também é de rotação.
Sendo assim os graus de liberdades da nossa viga serão.
Somando um total de 3 graus de liberdade. O que eles têm de especial? São todos graus de liberdade de rotação, e esses graus que chamamos de Deslocabilidades internas, ou seja, todo nó de uma estrutura que pode rotacionar, é contabilizado como deslocabilidades internas, e no nosso caso, essa viga possui 3 deslocabilidades internas.
OBS: Vale lembrar que sempre que tivermos um nó rotulado, a deslocabilidade interna dele será zero, ou seja, em nós rotulados considera-se o grau de liberdade de rotação inexistente.
Deslocabilidade externa
Agora vem o ponto legal, se as rotações marcam deslocabilidade interna, os deslocamentos vão marcar deslocabilidades externas, porém como vamos saber quantos são? É aqui que entra o nosso macetinho novamente, vamos ver a seguinte estrutura dada aqui embaixo.
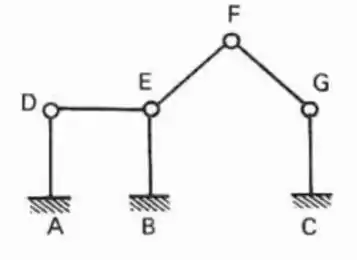
Perceba que nesse caso os nós D, E, F e G são rotulados, ou seja, todas as deslocabilidades internas aqui são nulas. Nos nós A, B e C temos engastes, ou seja, as deslocbilidades internas ali são impedidas, então na nossa estrutura não possuímos nenhuma deslocabilidade interna, vamos agora ponto a ponto vendo como a nossa estrutura se comporta:
Nó D
Vamos usar o mesmo conceito. Veja que se quisermos deslocar o nós D na vertical, não vamos conseguir porque o nó A trava ele.
Se quisermos rotacionar ele, já sabemos que que a rótula irá zerar a nossa deslocabilidade interna que temos ali.
Mas e se empurrarmos ou puxarmos ele na horizontal?
Veja que na horizontal ele não possui restrição, ou seja, pode deslocar. E se pode deslocar isso é um grau de liberdade, e aqui que acontece a mágica. Se rotações marcam deslocabilidades internas, deslocamentos marcam as deslocabilidades externas. Ou seja, se quisermos impedir o movimento horizontal do nó D, colocamos nele um apoio do primeiro gênero como ilustramos aqui em baixo:
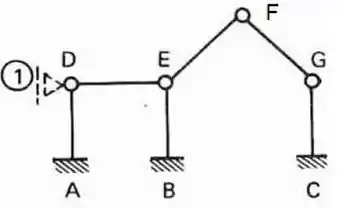
Assim o nosso D passou a ser indeslocavel como os Nós A, B e C, mas em troca ganhamos uma deslocabilidade externa.
Nó E
Fazendo a mesma análise para o Nó E temos que:
A rótula zera o nosso efeito de rotação, ou seja, desprezamos a nossa deslocabilidade interna.
Sabemos que verticalmente o nó B trava o nó E.
E horizontalmente? Ai que entra o segundo macete, em teoria na horizontal o nó E se movimenta, certo? Mas você não transformou o nó D em indeslocavel? Se o nó D e o nó B são indeslocaveis, e o nó E está ligado a eles, então podemos garantir que o nó E também é indeslocavel, e assim temos que o nó E não nós dará nenhuma deslocabilidade externa.
Nó G
Fui para o nó G porque perceba que ele está ligado ao nó C, que é indeslocavel.
Sendo assim já sabemos que o nó G não se desloca na vertical, porque o nó C impede isso.
Sabemos também que a rótula garante que também não teremos deslocabilidade interna.
Porém, veja que na horizontal o nó G pode se deslocar, ou seja, se pode se deslocar, vira uma deslocabilidade externa, e colocamos um apoio do primeiro gênero ali para impedir o movimento, sendo assim teremos que:
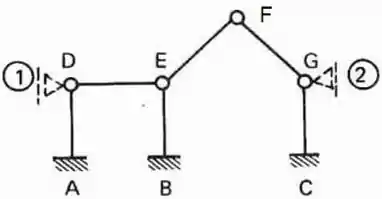
Ou seja, agora no total temos 2 deslocabilidades externas. Mas ainda falta um nó a ser averiguado.
Nó F
Esse é bem tranquilo, porque veja só.
Sabemos que em rotação a rótula já tira qualquer possibilidade de deslocabilidade interna.
Porém ele pode se movimentar na horizontal e na vertical, correto?
Poderia SE não tivéssemos o nó E e o nó G como nós indeslocaveis. Lembra que na nossa análise o nó E e o no G viraram indeslocaveis, e com isso, se o nó F está ligado a Nós indeslocaveis, automaticamente ele também se torna um nó indeslocavel.
Com isso nossa estrutura totaliza 2 deslocabilidades externas.
Número de deslocabilidades
O número de deslocabilidades nós dará o total de incógnitas a serem determinadas, e é bem simples fazer esse valor, é só somar o número de deslocabilidades externas e internas para obter o total de deslocabilidades, e assim teremos que:
Ufa, entendido isso, bora treinar alguns exercícios para podermos ficar craque em deslocabilidades externas e internas.
Nó A
Nó B
Nó C
Deslocabilidade externa
Nó D
Nó E
Nó G
Nó F
Número de deslocabilidades
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine o número de deslocabilidades (externas e internas da estrutura abaixo).
Passo 1
O número de deslocabilidades internas é bem simples de determinar, basta contabilizarmos nós que passam na seguinte regra:
- Os nós dos apoios não contam
- Os nós com rótulas também não contam
- Todos os outros nós serão contabilizados
Sendo assim temos que os nós que nem tem rótulas e não são apoios são os seguintes nós:
Então o número de deslocabilidades internas são:
Passo 2
O número de deslocabilidades externas, são aquelas relativas à movimentação da estrutura. Para isso devemos analisar cada um dos nós separadamente, então nomeando os nossos nós, teremos que:
- Nós e :
- Nó B
- Nó C
São apoios de segundo gênero, logo, não possuem nenhuma deslocabilidade externa.
O nó B não pode se deslocar na vertical, e a rotação dele já foi contabilizada como deslocabilidade interna, porém, ele pode se mover na horizontal, e sabemos que na direção que a estrutura pode se mover, colocamos um apoio do primeiro gênero representando a nossa deslocabilidade externa, sendo assim teremos:
Perceba que o nó C está ligado ao nó B e D, que são nós indeslocáveis (e perceba que só passamos a considera-los indeslocáveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó C não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada
Assim podemos ver que tivemos o seguinte número de deslocabilidades externas:
Passo 3
O total de deslocabilidades será dado por:
Resposta
Exercício Resolvido #2
Origem do Exercício
Determine o número de deslocabilidades (externas e internas da estrutura abaixo).
Passo 1
O número de deslocabilidades internas é bem simples de determinar, basta contabilizarmos nós que passam na seguinte regra:
- Os nós dos apoios não contam
- Os nós com rótulas também não contam
- Todos os outros nós serão contabilizados
Sendo assim temos que os nós que nem tem rótulas e não são apoios são os seguintes nós:
Então o número de deslocabilidades internas são:
Passo 2
O número de deslocabilidades externas, são aquelas relativas a movimentação da estrutura. Para isso devemos analisar cada um dos nós separadamente, então nomeando os nossos nós, teremos que:
- Nó A
- Nó B
- Nó E
- Nó D
- Nó C
O nó A é um engaste, logo, ele não possui nenhuma deslocabilidade externa.
O nó B não pode se deslocar na vertical, e a rotação dele já foi contabilizada como deslocabilidade interna, porém, ele pode se mover na horizontal, e sabemos que na direção que a estrutura pode se mover, colocamos um apoio do primeiro gênero representando a nossa deslocabilidade externa, sendo assim teremos:
O nó E é um indeslocável, logo, ele não possui nenhuma deslocabilidade externa.
O nó D não pode se deslocar na vertical, e a rotação dele já foi contabilizada como deslocabilidade interna, porém, ele pode se mover na horizontal, e sabemos que na direção que a estrutura pode se mover, colocamos um apoio do primeiro gênero representando a nossa deslocabilidade externa, sendo assim teremos:
Perceba que o nó C está ligado ao nó B e D, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó C não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada
Assim podemos ver que tivemos o seguinte número de deslocabilidades externas:
Passo 3
O total de deslocabilidades será dado por:
Resposta
Exercício Resolvido #3
Elaboração própria
Determine o número de deslocabilidades (externas e internas da estrutura abaixo).
Passo 1
O número de deslocabilidades internas é bem simples de determinar, basta contabilizarmos nós que passam na seguinte regra:
- Os nós dos apoios não contam
- Os nós com rótulas também não contam
- Todos os outros nós serão contabilizados
Sendo assim temos que os nós que nem tem rótulas e não são apoios são os seguintes nós:
Então o número de deslocabilidades internas são:
Passo 2
O número de deslocabilidades externas, são aquelas relativas à movimentação da estrutura. Para isso devemos analisar cada um dos nós separadamente, então nomeando os nossos nós, teremos que:
- Nós e :
- Nó B
- Nó D
São apoios de terceiro e segundo gênero, logo, não possuem nenhuma deslocabilidade externa.
O nó B não pode se deslocar na vertical, e a rotação dele já foi contabilizada como deslocabilidade interna, porém, ele pode se mover na horizontal, e sabemos que na direção que a estrutura pode se mover, colocamos um apoio do primeiro gênero representando a nossa deslocabilidade externa, sendo assim teremos:
O nó D não pode se deslocar na vertical, e a rotação dele já foi contabilizada como deslocabilidade interna, porém, ele pode se mover na horizontal, e sabemos que na direção que a estrutura pode se mover, colocamos um apoio do primeiro gênero representando a nossa deslocabilidade externa, sendo assim teremos
Assim podemos ver que tivemos o seguinte número de deslocabilidades externas:
Passo 3
O total de deslocabilidades será dado por:
Resposta
Exercício Resolvido #4
Origem do Exercício
Determine o número de deslocabilidades (externas e internas da estrutura abaixo).
Passo 1
O número de deslocabilidades internas é bem simples de determinar, basta contabilizarmos nós que passam na seguinte regra:
- Os nós dos apoios não contam
- Os nós com rótulas também não contam
- Todos os outros nós serão contabilizados
Sendo assim temos que os nós que nem tem rótulas e não são apoios são os seguintes nós:
Então o número de deslocabilidades internas são:
Passo 2
O número de deslocabilidades externas, são aquelas relativas a movimentação da estrutura. Para isso devemos analisar cada um dos nós separadamente, então nomeando os nossos nós, teremos que:
- Nó A
- Nó B
- Nó C
- Nó F e H
- Nó E
- Nó D
- Nó G
Perceba que o nó A apesar de ser um apoio, possui travamento apenas na vertical, podendo se mover na horizontal, logo, para evitar isso, o que devemos fazer? Isso mesmo, colocar um apoio do primeiro gênero ali, e assim temos a nossa primeira deslocabilidade externa, dessa forma teremos que:
O nó B não pode se deslocar na vertical, e a rotação dele já foi contabilizada como deslocabilidade interna, porém, ele pode se mover na horizontal, e sabemos que na direção que a estrutura pode se mover, colocamos um apoio do primeiro gênero representando a nossa deslocabilidade externa, sendo assim teremos:
O nó C não pode se deslocar na vertical, e a rotação dele já foi contabilizada como deslocabilidade interna, porém, ele pode se mover na horizontal, e sabemos que na direção que a estrutura pode se mover, colocamos um apoio do primeiro gênero representando a nossa deslocabilidade externa, sendo assim teremos:
O nó F e H são engastes, logo, eles não possuem nenhuma deslocabilidade externa.
Perceba que o nó E está ligado ao nó B e F, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó E não irá possuir deslocabilidades externas, e perceba que ele não possui deslocabilidade interna devido a rótula.
Perceba que o nó D está ligado ao nó C e E, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó D não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada
Perceba que o nó G está ligado ao nó E e H, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó G não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada
Assim podemos ver que tivemos o seguinte número de deslocabilidades externas:
Passo 3
O total de deslocabilidades será dado por:
Resposta
Exercício Resolvido #5
Origem do Exercício
Determine o número de deslocabilidades (externas e internas da estrutura abaixo).
Passo 1
O número de deslocabilidades internas é bem simples de determinar, basta contabilizarmos nós que passam na seguinte regra:
- Os nós dos apoios não contam
- Os nós com rótulas também não contam
- Todos os outros nós serão contabilizados
Sendo assim temos que os nós que nem tem rótulas e não são apoios são os seguintes nós:
Então o número de deslocabilidades internas são:
Passo 2
O número de deslocabilidades externas, são aquelas relativas a movimentação da estrutura. Para isso devemos analisar cada um dos nós separadamente, então nomeando os nossos nós, teremos que:
- Nó A, E e H
- Nó B
- Nó D
- Nó C
- Nó G
- Nó F
O nó A, E e H são um engaste, logo, eles não possuem nenhuma deslocabilidade externa.
O nó B não pode se deslocar na vertical, e a rotação dele já foi contabilizada como deslocabilidade interna, porém, ele pode se mover na horizontal, e sabemos que na direção que a estrutura pode se mover, colocamos um apoio do primeiro gênero representando a nossa deslocabilidade externa, sendo assim teremos:
Perceba que o nó D está ligado ao nó B e E, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó D não irá possuir deslocabilidades externas, e perceba que ele não possui deslocabilidade interna devido a rótula.
Perceba que o nó C está ligado ao nó B e D, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó C não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada
Perceba que o nó G está ligado ao nó D e H, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó G não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada
Perceba que o nó F está ligado ao nó D e G, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó F não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada
Assim podemos ver que tivemos o seguinte número de deslocabilidades externas:
Passo 3
O total de deslocabilidades será dado por:
Resposta
Exercício Resolvido #6
Origem do Exercício
Determine o número de deslocabilidades (externas e internas da estrutura abaixo).
Passo 1
O número de deslocabilidades internas é bem simples de determinar, basta contabilizarmos nós que passam na seguinte regra:
- Os nós dos apoios não contam
- Os nós com rótulas também não contam
- Todos os outros nós serão contabilizados
Sendo assim temos que os nós que nem tem rótulas e não são apoios são os seguintes nós:
Então o número de deslocabilidades internas são:
Passo 2
O número de deslocabilidades externas, são aquelas relativas a movimentação da estrutura. Para isso devemos analisar cada um dos nós separadamente, então nomeando os nossos nós, teremos que:
- Nó A, E e F
- Nó B
- Nó D
- Nó C
O nó A, E e F são um engaste, logo, eles não possuem nenhuma deslocabilidade externa.
Perceba que o nó B está ligado ao nó A e E, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó B não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada.
Perceba que o nó D está ligado ao nó B e F, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó D não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada.
Perceba que o nó C está ligado ao nó B e D, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó C não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada.
Assim podemos ver que tivemos o seguinte número de deslocabilidades externas:
Passo 3
O total de deslocabilidades será dado por:
Resposta
Exercício Resolvido #7
Origem do Exercício
Determine o número de deslocabilidades (externas e internas da estrutura abaixo).
Passo 1
O número de deslocabilidades internas é bem simples de determinar, basta contabilizarmos nós que passam na seguinte regra:
- Os nós dos apoios não contam
- Os nós com rótulas também não contam
- Todos os outros nós serão contabilizados
Sendo assim temos que os nós que nem tem rótulas e não são apoios são os seguintes nós:
Aqui vale explicar uma coisa. Perceba que não marcamos a rótula, porque já sabemos que a rótula não dá deslocabilidades internas. Porém preste muito a atenção, porque nesse caso a rótula pertence apenas a barra que está na horizontal, e essa barra horizontal encosta na barra vertical exatamente pela rótula. Ou seja, a barra vertical terá uma deslocabilidade interna, mas a horizontal não, sendo assim teremos que o total de deslocabilidades internas é:
Passo 2
O número de deslocabilidades externas, são aquelas relativas a movimentação da estrutura. Para isso devemos analisar cada um dos nós separadamente, então nomeando os nossos nós, teremos que:
- Nó A, C e D
- Nó B
O nó A, C e D são um engaste, logo, eles não possuem nenhuma deslocabilidade externa.
Perceba que o nó B está ligado aos nós A, C e D, que são nós indeslocaveis (e perceba que só passamos a considera-los indeslocaveis após termos colocado o apoio do primeiro gênero). Sendo assim, o nosso nó B não irá possuir deslocabilidades externas, possuindo apenas a deslocabilidade interna que já foi contabilizada.
Assim podemos ver que tivemos o seguinte número de deslocabilidades externas:
Passo 3
O total de deslocabilidades será dado por:
Resposta
Exercício Resolvido #8
Elaboração própria
Determine o número de deslocabilidades (externas e internas da estrutura abaixo).
Passo 1
O número de deslocabilidades internas é bem simples de determinar, basta contabilizarmos nós que passam na seguinte regra:
- Os nós dos apoios não contam
- Os nós com rótulas também não contam
- Todos os outros nós serão contabilizados
Sendo assim temos que os nós que nem tem rótulas e não são apoios são os seguintes nós:
Aqui vale explicar uma coisa. Perceba que não marcamos a rótula, porque já sabemos que a rótula não dá deslocabilidades internas. Porém preste muito a atenção, porque nesse caso a rótula pertence apenas a barra que está na horizontal, e essa barra horizontal encosta na barra vertical exatamente pela rótula. Ou seja, a barra vertical terá uma deslocabilidade interna, mas a horizontal não, sendo assim teremos que o total de deslocabilidades internas é:
Passo 2
O número de deslocabilidades externas, são aquelas relativas a movimentação da estrutura. Para isso devemos analisar cada um dos nós separadamente, então nomeando os nossos nós, teremos que:
- Nó D e F
- Nó A
- O nó B também permite deslocamento em então também admite uma deslocabildiade externa:
- Com isso os nós e não permitem mais deslocabilidades.
O nó D e F são engastes, logo, eles não possuem nenhuma deslocabilidade externa.
O nó A permite deslocamento em logo possui uma deslocabilidade externa:
Assim podemos ver que tivemos o seguinte número de deslocabilidades externas:
Passo 3
O total de deslocabilidades será dado por:
Resposta
