Deslocamento em Estruturas Isostáticas – Revisão de Trabalhos Virtuais
Teoria
Porque estruturas isostáticas?
Você pode estar se perguntando: por que o primeiro tópico de estruturas hiperestáticas é exatamente estruturas isostáticas?
É bem importante entendermos o funcionamento das estruturas isostáticas antes de partirmos para as hiperestáticas, pois todo o conceito de hiperestaticidade vai girar entorno de resolver vários arranjos isostáticos.Por isso vale nos preocuparmos com isso logo de início, mas agora chega de ladainha e vamos partir para o que interessa...
O principio dos trabalhos virtuais em estruturas isostáticas.
Imagine a seguinte situação:
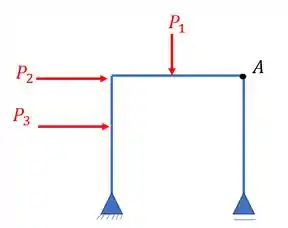
Temos na figura acima um pórtico sujeito a diversos tipos de carregamentos e queremos saber como o ponto A do nosso pórtico irá se comportar. Sabemos que analisar o ponto A como todos os carregamentos (1,2,3) de maneira direta seria muito complicado, então usamos um artificio de analise virtual. Imagine que ao invés de usar todas essas cargas, eu pudesse dizer o seguinte:
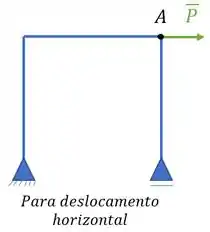
Suponha que eu queira saber o deslocamento horizontal de A... nesse caso imagine que eu pudesse representar todas as minhas forças da primeira figura em uma única força que atue na direção do deslocamento que eu queira conhecer, e que, nesse caso, eu estou garantindo que o carregamento (ou seja, unitário) produz na estrutura o mesmo deslocamento que todas as cargas da figura anterior. Ou seja, o carregamento unitário VIRTUAL horizontal que age em A produz o mesmo deslocamento horizontal que as Cargas REAIS (, , ).
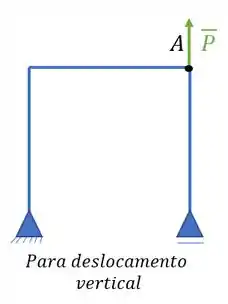
E isso é bem importante, se eu quiser saber o deslocamento vertical em A, eu coloco uma carga unitária na direção vertical, e pode ser pra cima ou pra baixo, o sinal do seu deslocamento é quem vai te dizer qual o certo.
Por exemplo, se você colocar uma carga unitária vertical pra cima, e quando calcular o seu deslocamento ele der negativo, significa que ele se moveu pra baixo, que é o sentido contrario do que você colocou a carga. Se der positivo, se deslocou no mesmo sentido do carregamento unitário.
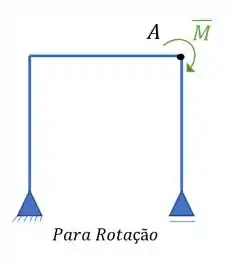
E se quiser saber a rotação em A, aplico um momento unitário nesse ponto.
Beleza, sabendo disso, o que eu preciso fazer agora é entender como isso funciona na ideia de trabalho virtual.
Trabalho externo e interno
Sabemos que os carregamentos externos e internos irão produzir energia, e como nosso objetivo é sempre equilibrar as coisas, temos que garantir que haja equilíbrio entre as parcelas de trabalho interno e de trabalho externo.
Eu poderia passar aqui um tempão desenvolvendo a fórmula pra vocês, ou eu posso simplesmente ensinar pra vocês um macete sagaz... obvio que vou ficar com a segunda opção hehehe
O macete sagaz é o seguinte:
- Como vimos, analisar o deslocamento na estrutura com a carga virtual, é bem mais simples, logo, é mais fácil determinar o trabalho virtual externo nessa estrutura, dessa maneira temos que:
- Para calcular o trabalho interno, existe uma fórmula de resistência dos materiais que nos auxilia, que a sua forma final é dada por:
- trabalho devido a esforço cortante
- trabalho devido a esforço torsor
- trabalho devido a esforço normal
- trabalho devido a esforço Momento
Meu deus do céu, que diabo de fórmula é essa? Fica tranquilo que vou explicar cada termo dela.
Mas antes lembra que para termos equilíbrio, basta igualarmos as duas fórmulas, e com isso temos que:
Trabalho interno
Pra tudo ficar bem claro, a gente tem que entender o seguinte: para fazer uma comparação que vai explodir a sua cabeça, lembra do conceito de vetor unitário da física.
O que é um vetor unitário? Nada mais é que um vetor de tamanho 1 que representa o que acontece com um vetor maior, por exemplo, se eu escrever.
Significa que eu tenho um vetor de tamanho 20 que está na direção X. ou seja, o vetor unitário não modifica o vetor 20, só da um sentido e uma direção pra ele, e como ele é unitário, tudo que eu multiplicar por ele, não é alterado.
Acho que você já pegou a ideia né? É exatamente isso que temos na nossa fórmula. Todos os termos com uma barra em cima (,e são “tipo” um vetor unitário, eles só vão nós auxiliar no cálculo. Os outros termos sem barra são os valores com os carregamentos reais na estrutura, que, no nosso exemplo, seria o valor 20.
Ou seja, todos os valores com barras em cima são uma espécie de vetor unitário, e todos os valores sem barra são os reais, como o 20 do nosso exemplo. Entendido isso, eu tenho uma novidade ainda melhor pra você. Dificilmente usamos essa fórmula com seu tamanho total. Quer ver como usar ela? Então segue o bonde.
Como usar cada termo?
Vamos começar pelo que parece mais difícil.
Essa fórmula pode ser desprezada, porque a contribuição dela para os deslocamentos é praticamente zero (e basicamente nunca usamos ela nos nossos problemas). Pode falar que você já ficou feliz de saber isso né? Só pra você não ficar com a pulga atrás da orelha, vamos ver o que significa cada termo.
Essa fórmula é bem específica, e ela basicamente só é usada em problemas de grelhas tridimensionais, ou em estruturas com ação de torque. Cada termo da nossa fórmula significa:
Essa a gente, pra dizer a verdade, só é usada em treliças, dificilmente usamos em outros tipos de estruturas, ou seja, só usamos ela em estruturas que funcionem prioritariamente com esforços normais, e no nosso caso as treliças fazem esse papel. Vele lembrar que nesse caso a parcelo devido aos momentos também pode ser desprezada no caso de treliças, e com isso a nossa fórmula para treliças fica sendo:
Mas você pode me perguntar, e se minha treliça tiver 3 barras? Ai é só fazer três integrais, uma pra cada barra, e igualar ao trabalho externo, e você irá ter isso aqui:
E claro que se as barras forem todas iguais, a nossa fórmula fica sendo
Em que cada termo da nossa fórmula representa o seguinte
Essa é o que a gente mais vai usar, usamos ela em estruturas tipo pórticos, grelhas, e treliças com cargas fora do nó que não possuam tirantes. Vale lembrar que geralmente quando se tem esforço de momento fletor, todas as outras três parcelas são desprezadas, com isso a nossa fórmula passa a ser.
Mas você pode me perguntar, e se meu pórtico tiver 3 barras? Ai é só fazer três integrais, uma pra cada barra, e igualar ao trabalho externo, e você irá ter isso aqui:
E claro que se as barras forem todas iguais, a nossa fórmula fica sendo
Em que cada termo da nossa fórmula representa o seguinte
Mas como é de lei, pra pegarmos bem a ideia da fórmula vamos fazer exercício, então chega mais e bora fazer uns exercícios pra isso ficar bem clarão na nossa cabeça.
Trabalho externo e interno
Trabalho interno
Como usar cada termo?
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
Calcule o deslocamento horizontal de D, para o pórtico abaixo. Usar para todas as barras
Passo 1
Como queremos saber o deslocamento da nossa estrutura já sabemos que antemão que podemos usar a seguinte fórmula
Sabemos também que em pórticos sem tirantes podemos desprezar as outras três parcelas (devido ao normal, ao cortante e ao torque). Com isso nossa fórmula passa a ser.
Como temos 3 barras a nossa conta fica da seguinte maneira:
E como todas as barras possuem o mesmo módulo de elasticidade e o mesmo momento polar de inércia, a nossa fórmula fica sendo, de maneira simplificada o seguinte.
Em que precisamos determinar os diagramas de momento fletor tanto para o caso unitário quanto para o caso real.
Passo 2
Como queremos determinar o deslocamento unitário na direção A, basta aplicarmos uma carga unitária no ponto em que se deseja determinar o deslocamento, e na direção desejada, nesse caso, na direção horizontal.
Fazendo o diagrama de corpo livre temos que a reação de apoio será dada por
Tendo as reações de apoio traçamos o diagrama de momentos fletores do pórtico devido a carga unitária (não iremos detalhar essa parte nessa aula, mas falamos muito sobre isso no tópico solução de pórticos simples no assunto Treliças e estruturas isostáticas)
Perceba que o pórtico foi desenhado separado com o intuito de facilitar o desenho. O diagrama foi desenhado na direção das fibras tracionadas, que nesse caso são as fibras internas, e veja que podemos escrever os diagramas de momentos como uma função do comprimento de cada barra, e dessa maneira teremos a seguinte representação.
E assim deixamos pronto o diagrama de momentos devido a cargas unitárias.
Passo 3
Agora precisamos fazer o mesmo diagrama para a estrutura real do nosso problema. Nossa estrutura real é:
Calculando as reações de apoios teremos que:
Com as reações de apoio podemos determinar os diagramas de momentos fletores
Perceba que o pórtico foi desenhado separado com o intuito de facilitar o desenho. O diagrama foi desenhado na direção das fibras tracionadas, que nesse caso são as fibras internas, e veja que podemos escrever os diagramas de momentos como uma função do comprimento de cada barra, e dessa maneira teremos a seguinte representação.
E assim deixamos pronto o diagrama de momentos devido a cargas reais.
Passo 4
Agora basta juntarmos na nossa fórmula cada uma das equações encontradas
perceba que o deslocamento deu positivo, ou seja, arbitramos a carga unitária na direção correta de deformação, e por isso tivemos um valor positivo.
Resposta
Exercício Resolvido #2
Origem do Exercício
Calcule a rotação do ponto A, para a viga abaixo. Usar para toda a viga
Passo 1
Como queremos saber o deslocamento da nossa estrutura já sabemos que antemão que podemos usar a seguinte fórmula
Sabemos também que em vigas podemos desprezar três parcelas (devido ao normal, ao cortante e ao torque). Com isso nossa fórmula passa a ser.
Como temos 1 viga com dois trechos podemos escrever a equação da seguinte maneira.
E como todas as barras possuem o mesmo módulo de elasticidade e o mesmo momento polar de inércia, a nossa fórmula fica sendo, de maneira simplificada o seguinte.
Em que precisamos determinar os diagramas de momento fletor tanto para o caso unitário quanto para o caso real.
Passo 2
Como queremos determinar o deslocamento unitário na direção A, basta aplicarmos uma carga unitária no ponto em que se deseja determinar o deslocamento, e na direção desejada, nesse caso, uma rotação em A.
Fazendo o diagrama de corpo livre temos que a reação de apoio será dada por
Tendo as reações de apoio traçamos o diagrama de momentos fletores da viga devido a carga unitária (não iremos detalhar essa parte nessa aula, mas falamos muito sobre isso no tópico solução de vigas simples no assunto Treliças e estruturas isostáticas)
O diagrama foi desenhado na direção das fibras tracionadas, que nesse caso são as fibras inferiores, e veja que podemos escrever os diagramas de momentos como uma função do comprimento da barra, e dessa maneira teremos a seguinte representação.
E assim deixamos pronto o diagrama de momentos devido a cargas unitárias.
Passo 3
Agora precisamos fazer o mesmo diagrama para a estrutura real do nosso problema. Nossa estrutura real é:
Calculando as reações de apoios teremos que:
Com as reações de apoio podemos determinar os diagramas de momentos fletores
O diagrama foi desenhado na direção das fibras tracionadas, que nesse caso são as fibras inferiores do lado direito e as superiores do lado esquerdo, e veja que podemos escrever os diagramas de momentos como uma função do comprimento de cada trecho, e dessa maneira teremos a seguinte representação.
E assim deixamos pronto o diagrama de momentos devido a cargas reais. Perceba que tanto no diagrama de momentos de carga unitária, quanto no diagrama de momentos fletores reais, estamos considerando os momentos que tracionam as fibras da parte de cima como negativos, e os momentos que tracionam as fibras inferiores como positivo. Você vai perceber que substituindo nas equações, sempre que tivermos tração em cima, a equação vai dar negativa, e sempre que estiver embaixo vai da positiva.
Passo 4
Agora basta juntarmos na nossa fórmula cada uma das equações encontradas
perceba que a rotação deu negativa, ou seja, arbitramos a carga unitária na direção inversa do que de fato a estrutura rotaciona, e por isso tivemos um valor negativo.
Resposta
Exercício Resolvido #3
Origem do Exercício
Calcule o deslocamento vertical do ponto A, para a viga abaixo. Usar para toda a viga
Passo 1
Como queremos saber o deslocamento da nossa estrutura já sabemos que antemão que podemos usar a seguinte fórmula
Sabemos também que em vigas podemos desprezar três parcelas (devido ao normal, ao cortante e ao torque). Com isso nossa fórmula passa a ser.
Como temos 1 viga com um único trecho podemos escrever a equação da seguinte maneira.
E como todas as barras possuem o mesmo módulo de elasticidade e o mesmo momento polar de inércia, a nossa fórmula fica sendo, de maneira simplificada o seguinte.
Em que precisamos determinar os diagramas de momento fletor tanto para o caso unitário quanto para o caso real.
Passo 2
Como queremos determinar o deslocamento unitário na direção A, basta aplicarmos uma carga unitária no ponto em que se deseja determinar o deslocamento, e na direção desejada, nesse caso, uma carga vertical em A.
Fazendo o diagrama de corpo livre temos que a reação de apoio será dada por
Tendo as reações de apoio traçamos o diagrama de momentos fletores da viga devido a carga unitária (não iremos detalhar essa parte nessa aula, mas falamos muito sobre isso no tópico solução de vigas simples no assunto Treliças e estruturas isostáticas)
O diagrama foi desenhado na direção das fibras tracionadas, que nesse caso são as fibras superiores, e veja que podemos escrever os diagramas de momentos como uma função do comprimento da barra, e dessa maneira teremos a seguinte representação.
E assim deixamos pronto o diagrama de momentos devido a cargas unitárias. E perceba que a nossa equação da reta precisa respeitar o sinal do momento fletor. Então, como sabemos, toda vez que tracionamos a parte de cima das fibras, consideramos isso negativo, por isso tome muito cuidado ao fazer a equação da reta da sua estrutura.
Passo 3
Agora precisamos fazer o mesmo diagrama para a estrutura real do nosso problema. Nossa estrutura real é:
Calculando as reações de apoios teremos que:
Com as reações de apoio podemos determinar os diagramas de momentos fletores
O diagrama foi desenhado na direção das fibras tracionadas, que nesse caso são as fibras superiores e veja que podemos escrever os diagramas de momentos como uma função do comprimento, e dessa maneira teremos a seguinte representação.
E assim deixamos pronto o diagrama de momentos devido a cargas reais. Perceba que tanto no diagrama de momentos de carga unitária, quanto no diagrama de momentos fletores reais, estamos considerando os momentos que tracionam as fibras da parte de cima como negativos, e os momentos que tracionam as fibras inferiores como positivo. Você vai perceber que substituindo nas equações, sempre que tivermos tração em cima, a equação vai dar negativa, e sempre que estiver embaixo vai da positiva.
Passo 4
Agora basta juntarmos na nossa fórmula cada uma das equações encontradas
perceba que o deslocamento deu positivo, ou seja, arbitramos a carga unitária na direção correta do que de fato a estrutura se movimenta, e por isso tivemos um valor positivo.
Resposta
Exercício Resolvido #4
Origem do Exercício
Calcule o deslocamento horizontal do ponto B, para a treliça abaixo. Usar para todas as barras da treliça:
Passo 1
Como queremos saber o deslocamento da nossa estrutura já sabemos que antemão que podemos usar a seguinte fórmula
Sabemos também que em treliças podemos desprezar três parcelas (devido ao momento, ao cortante e ao torque). Com isso nossa fórmula passa a ser.
Como temos várias barras, iremos precisar calcular o diagrama de todas elas, logo teremos
E como todas as barras possuem o mesmo módulo de elasticidade e a mesma área, a nossa fórmula fica sendo, de maneira simplificada o seguinte.
Em que precisamos determinar os diagramas normais tanto para o caso unitário quanto para o caso real.
Passo 2
Como queremos determinar o deslocamento horizontal, basta aplicarmos uma carga unitária no ponto em que se deseja determinar o deslocamento, e na direção desejada, nesse caso, uma carga horizontal em B.
Fazendo o diagrama de corpo livre temos que a reação de apoio será dada por
Tendo as reações de apoio traçamos o diagrama de normais da treliça devido a carga unitária (não iremos detalhar essa parte nessa aula, mas falamos muito sobre isso no tópico solução de treliças no assunto Treliças e estruturas isostáticas)
Perceba que alguns normais são iguais a zeros, o que podemos usar para simplificar a nossa equação, sabemos que:
Logo a nossa equação será
E lembre-se que no caso de treliças as equações dos normais serão constantes, que serão escritos como:
Passo 3
Agora precisamos fazer o mesmo diagrama para a estrutura real do nosso problema. Nossa estrutura real é:
Calculando as reações de apoios teremos que:
Com as reações de apoio podemos determinar os diagramas de normais
Perceba que com a nossa equação simplificada só iremos precisar do valor de duas barras, que são:
Passo 4
Precisamos determinar o comprimento de cada uma das barrinhas da nossa treliça, para podermos substituir tudo na nossa fórmula. Fazendo Pitágoras vamos encontrar que:
Passo 5
Agora basta juntarmos na nossa fórmula cada uma das equações encontradas
perceba que o deslocamento deu positivo, ou seja, arbitramos a carga unitária na direção correta do que de fato a estrutura se movimenta, e por isso tivemos um valor positivo.
Resposta
Exercício Resolvido #5
Origem do Exercício
Calcule o deslocamento vertical do ponto C, para a treliça abaixo. Usar para todas as barras da treliça:
Passo 1
Como queremos saber o deslocamento da nossa estrutura já sabemos que antemão que podemos usar a seguinte fórmula
Sabemos também que em treliças podemos desprezar três parcelas (devido ao momento, ao cortante e ao torque). Com isso nossa fórmula passa a ser.
Como temos várias barras, iremos precisar calcular o diagrama de todas elas, logo teremos
E como todas as barras possuem o mesmo módulo de elasticidade e a mesma área, a nossa fórmula fica sendo, de maneira simplificada o seguinte.
Em que precisamos determinar os diagramas normais tanto para o caso unitário quanto para o caso real.
Passo 2
Como queremos determinar o deslocamento vertical na direção vertical, basta aplicarmos uma carga unitária no ponto em que se deseja determinar o deslocamento, e na direção desejada, nesse caso, uma vertical em C.
Fazendo o diagrama de corpo livre temos que a reação de apoio será dada por
Tendo as reações de apoio traçamos o diagrama de normais da treliça devido a carga unitária (não iremos detalhar essa parte nessa aula, mas falamos muito sobre isso no tópico solução de treliças no assunto Treliças e estruturas isostáticas)
Perceba que alguns normais são iguais a zeros, o que podemos usar para simplificar a nossa equação, sabemos que:
Logo a nossa equação será
E lembre-se que no caso de treliças as equações dos normais serão constantes, que serão escritos como:
Passo 3
Agora precisamos fazer o mesmo diagrama para a estrutura real do nosso problema. Nossa estrutura real é:
Calculando as reações de apoios teremos que:
Com as reações de apoio podemos determinar os diagramas de normais
Perceba que com a nossa equação simplificada só iremos precisar do valor de 4 barras, que são:
Passo 4
Precisamos determinar o comprimento de cada uma das barrinhas da nossa treliça, para podermos substituir tudo na nossa fórmula. Fazendo Pitágoras vamos encontrar que:
Passo 5
Agora basta juntarmos na nossa fórmula cada uma das equações encontradas
perceba que o deslocamento deu positivo, ou seja, arbitramos a carga unitária na direção correta do que de fato a estrutura se movimenta, e por isso tivemos um valor positivo.
Resposta
Exercício Resolvido #6
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 534. Problema 14.25 (Adaptado)
Determine o deslocamento horizontal do ponto . Utilizar
Passo 1
Fala aí, pessoal!!! Olha só para começar esse exercício a gente precisa entender que o ponto é um apoio com liberdade para deslizar horizontalmente e o problema quer exatamente isso, o deslocamento horizontal de !!
Para resolver isso vamos utilizar aquela nossa equaçãozinha de trabalho virtual:
Mas a gente tem que lembrar também que para treliças a gente pode desprezar as parcelas: do momento, do cortanto e do torque; e obter:
Passo 2
Para resolver a equação acima a gente precisa dividir ela em cada seção da treliça, dessa forma vamos ter:
Vale lembrar que o termo é constante e igual para todos, logo:
Agora a gente vai precisar achar as normais virtuais e as normais reais para cada barra (você pode chamar de normais normais que fica mais legal também uahsuashuashusa)
Passo 3
Para achar as normais virtuais a gente vai aplicar uma força horizontal unitária em da seguinte forma:
Aplicamos em porque queremos o deslocamento em . É horizontal porque queremos o deslocamento horizontal. É unitária porque é SEMPRE unitária!
Pessoal, como o foco desse conteúdo não é ficar calculando reações e normais eu vou mostrar direto aqui quais serão esses valores:
Então vamos ter o seguinte:
Passo 4
Agora vamos achar as normais reais, vamos fazer isso utilizando o carregamento fornecido:
Novamente eu vou mostrar a vocês o resultado final, lembrando que o foco desse tópico não é ficar calculando essas reações e normais:
Então vamos ter o seguinte:
Passo 5
Agora a gente tem que achar os comprimentos de cada barra:
Passo 6
Agora é só substituir na equação:
Lembrando que o termo
Resposta
Exercício Resolvido #7
Elaboração própria
Determine o deslocamento vertical do ponto . Utilizar
Passo 1
Fala aí, pessoal!!! Olha só para começar esse exercício a gente precisa entender que o ponto tem liberdade para se mover tanto horizontalmente quanto verticalmente e o problema quer saber o deslocamento vertical de !!
Para resolver isso vamos utilizar aquela nossa equaçãozinha de trabalho virtual:
Mas a gente tem que lembrar também que para treliças a gente pode desprezar as parcelas: do momento, do cortanto e do torque; e obter:
Passo 2
Para resolver a equação acima a gente precisa dividir ela em cada seção da treliça, dessa forma vamos ter:
Vale lembrar que o termo é constante e igual para todos, logo:
Agora a gente vai precisar achar as normais virtuais e as normais reais para cada barra (você pode chamar de normais normais que fica mais legal também uahsuashuashusa)
Passo 3
Para achar as normais virtuais a gente vai aplicar uma força horizontal unitária em da seguinte forma:
Aplicamos em porque queremos o deslocamento em . É vertical porque queremos o deslocamento vertical. É unitária porque é SEMPRE unitária!
Pessoal, como o foco desse conteúdo não é ficar calculando reações e normais eu vou mostrar direto aqui quais serão esses valores:
Então vamos ter o seguinte:
Passo 4
Agora vamos achar as normais reais, vamos fazer isso utilizando o carregamento fornecido:
Novamente eu vou mostrar a vocês o resultado final, lembrando que o foco desse tópico não é ficar calculando essas reações e normais:
Então vamos ter o seguinte:
Passo 5
Agora é só substituir na equação:
Lembrando que o termo
Resposta
Exercício Resolvido #8
Elaboração própria
Determine o deslocamento vertical do ponto . Utilizar
Passo 1
Fala aí, pessoal!!! Olha só para começar esse exercício a gente precisa entender que o ponto tem liberdade para se mover tanto horizontalmente quanto verticalmente e o problema quer saber o deslocamento vertical de !!
Para resolver isso vamos utilizar aquela nossa equaçãozinha de trabalho virtual:
Mas a gente tem que lembrar também que para treliças a gente pode desprezar as parcelas: do momento, do cortanto e do torque; e obter:
Passo 2
Para resolver a equação acima a gente precisa dividir ela em cada seção da treliça, dessa forma vamos ter:
Vale lembrar que o termo é constante e igual para todos, logo:
Agora a gente vai precisar achar as normais virtuais e as normais reais para cada barra (você pode chamar de normais normais que fica mais legal também uahsuashuashusa)
Passo 3
Para achar as normais virtuais a gente vai aplicar uma força horizontal unitária em da seguinte forma:
Aplicamos em porque queremos o deslocamento em . É vertical porque queremos o deslocamento vertical. É unitária porque é SEMPRE unitária!
Pessoal, como o foco desse conteúdo não é ficar calculando reações e normais eu vou mostrar direto aqui quais serão esses valores:
Então vamos ter o seguinte:
Passo 4
Agora vamos achar as normais reais, vamos fazer isso utilizando o carregamento fornecido:
Novamente eu vou mostrar a vocês o resultado final, lembrando que o foco desse tópico não é ficar calculando essas reações e normais:
Então vamos ter o seguinte:
Passo 5
Agora é só substituir na equação:
Lembrando que então esse termo não precisa nem entrar. Além disso, vamos ter que as normais em e são idênticas então vamos agregar como
Lembrando que o termo
As distâncias são: e