Deslocamento em estruturas isostáticas- Temperatura e Recalque.
Teoria
Introdução
Como vimos nos casos anteriores, aprendemos a identificar como calcular os recalques em estruturas que sofrem a ação de uma força nela, nessa aula iremos aprender como calcular os recalques em estruturas que estão submetidas a variação de temperatura e recalques. Então vamos nessa.
Temperatura
Deslocamento em estruturas isostáticas devido a temperatura possui uma fórmula especifica, que é dada por:
Em que cada termo da fórmula significa:
- e
- Sinais
- NORMAIS
- MOMENTOS FLETORES
Carga unitária virtual que age na nossa estrutura no ponto que queremos saber o deslocamento na direção que queremos saber o deslocamento
Normal que age em cada barra da estrutura causado pela carga unitária virtual colocada no ponto que se deseja saber o deslocamento e na direção do deslocamento.
O nosso velho amigo coeficiente de dilatação térmico.
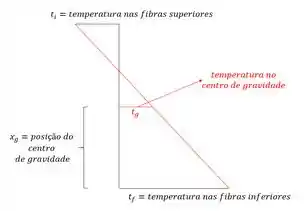
Temperatura no centro de gravidade da estrutura.
Momento Fletor que age em cada barra da estrutura causado pela carga unitária virtual colocada no ponto que se deseja saber o deslocamento e na direção do deslocamento.
Variação de temperatura entre as fibras da parte superior e da parte inferior das barras que compõem a estrutura.
Altura da seção das barras que compõem a estrutura.
Macete
Esse macete é bem legal. Se você garantir que todas as barras da estrutura possuem seção constante, podemos escrever a nossa fórmula como.
E agora pensa comigo, o que é a integral de um gráfico em seu comprimento? É exatamente a área desse gráfico. Ou seja, se as barras da estrutura possuem seção constante, basta calcular a área de cada gráfico de normal e momento por barra e multiplicar pelos seus respectivos coeficientes, e com isso a nossa fórmula vira.
Se olharmos o nosso exemplo aqui em baixo isso fica bem mais claro (supondo todas as barras com seção constante). E supondo que colocamos uma caga unitária em um determinado ponto, e essa carga unitária deu origem aos diagramas representados aqui embaixo.
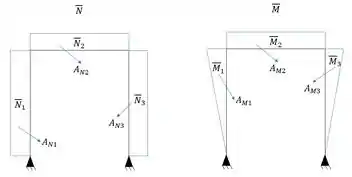
Que reescrevendo a nossa fórmula teremos que:
Agora ficou mais fácil 😉
Variação uniforme de temperatura
Se por acaso falarem que a variação de temperatura na estrutura é uniforme, isso significa que tanto as fibras da parte de baixo, quanto as fibras da parte de cima sofreram a mesma variação de temperatura, e por consequência estão na mesma temperatura, com isso, se a temperatura em cima e embaixo das fibras é igual, podemos garantir então que , e com isso a nossa fórmula passa a ser.
Em que já sabemos que se todas as barras possuírem seção constante, poderemos escrever a nossa fórmula como:
Obs: lembrar que a variação constante de temperatura some com , mas a temperatura no centro de gravidade () continua existindo.
Recalque
Deslocamento em estruturas isostáticas devido a recalque possui uma fórmula especifica, que é dada por:
Em que cada termo da fórmula significa:
Carga unitária virtual que age na nossa estrutura no ponto que queremos saber o deslocamento na direção que queremos saber o deslocamento
Esses caras eu coloquei junto porque é muito importante entender o funcionamento junto desses caras.
são as reações de apoio da nossa estrutura quando colocamos uma carga unitária no ponto que queremos saber o deslocamento e na direção que queremos conhecer o deslocamento.
está ligado a e a sua direção, ou seja, os recalques verticais em cada apoio estão ligados as reações verticais em cada apoio, assim como as deformações horizontais estão ligadas as reações horizontais, sempre respeitando o recalque com a reação correspondente, você pode estar se perguntando, como assim? Vamos ver um exemplo que fica tudo mais fácil.
Exemplo
Supondo que queremos saber o deslocamento horizontal no ponto C, sabendo que a estrutura sofreu um deslocamento vertical pra cima em A, horizontal para esquerda em A e um deslocamento vertical pra baixo em B.
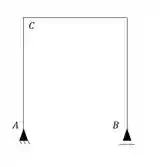
Passo 1
Por uma carga unitária no ponto em que se deseja saber o deslocamento e na direção que se deseja conhecer o deslocamento.
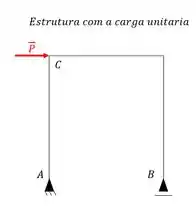
Passo 2
Determinamos as reações de apoio da estrutura devido a ação dessa carga unitária
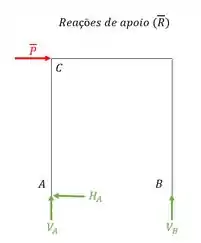
Passo 3
E esse passo é bem importante de se prestar atenção, pois desenhamos na estrutura a direção e o sentido dos recalques que foram apresentados no enunciado.
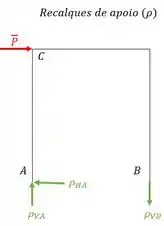
Resumo do que foi feito até aqui
Basicamente a sequencia de passos é a que vemos aqui embaixo.
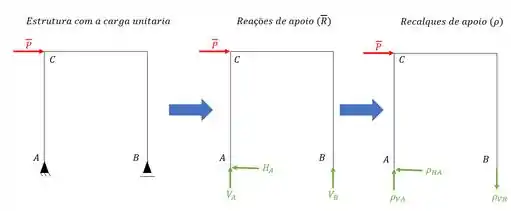
Passo 4
Agora precisamos ficar bem atentos, a nossa fórmula é
E como eu disse, precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
Sempre que a reação for no mesmo sentido do recalque, ela será positiva, e sempre que for no sentido contrário, será negativa.
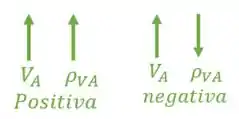
Passo 5
Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Perceba que os termos e são positivos pois estão na mesmo sentido, enquanto que é negativo pois está em sentidos opostos de atuação com relação ao recalque.
OBS: É MUITO IMPORTANTE TOMAR CUIDADO COM O SINAL DAS ÁREAS, ENTÃO PRA FICAR BEM FACIL SEMPRE LMEBRE DO SEGUINTE.
Sempre que for compressão o sinal da área será negativo, e sempre que for tração o sinal da área será positivo.
Sempre que os momentos fletores tracionarem as fibras da parte de cima, ou as fibras externas, o sinal da área vai ser negativo, mas se tracionar as fibras da parte de baixo, ou as fibras internas, o sinal das áreas vai ser positivo.
Tome muito cuidado para não errar os sinais.
Agora ficou muito mais fácil né? Então bora fazer exercício.
Macete
Variação uniforme de temperatura
Recalque
Exemplo
Passo 1
Passo 2
Passo 3
Resumo do que foi feito até aqui
Passo 4
Passo 5
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Supondo que o apoio A sofreu um deslocamento vertical para cima de , e o apoio B sofreu um deslocamento vertical para baixo de . Determine o deslocamento vertical do ponto C do pórtico.
Passo 1
Fala aí, galerinha!!! Esse problema trata sobre recalques, recalque é outra forma de dizer que houve um deslocamento, beleza?
Depois que esses deslocamentos descritos no enunciado aconteceram o nosso pórtico vai mudar e outros pontos também irão se deslocar, correto? O problema quer saber qual será o deslocamento final do ponto .
Para isso vamos utilizar nossa equaçãozinha de recalque:
Nós vamos debater sobre como utilizar essa equação conforme formos resolvendo o exercício, de qualquer forma o importante agora é lembrar que:
- Devemos aplicar uma carga unitária em .
- Calcular as reações dos apoios devido à carga unitária.
- Analisar os deslocamentos dados.
- Colocar tudo isso dentro da equação
Passo 2
A primeira coisa que devemos fazer é pôr uma carga unitária no ponto em que se deseja saber o deslocamento e na direção que se deseja conhecer o deslocamento. No nosso caso é no ponto C e vertical para baixo. Vamos aproveitar e representar as forças de reação nos apoios também.
Passo 3
Agora nós vamos analisar os deslocamentos dados. Isso consiste em colocar no nosso pórtico os deslocamentos fornecidos no problema ().
Passo 4
Agora precisamos ficar bem atentos, a nossa fórmula é
Aqui precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,
e sempre que for no sentido contrário, será negativa.
Passo 5
Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Substituindo os valores e lembrando que nossa carga unitária vale
O sinal negativo significa que o deslocamento se dá no sentido inverso da força unitária aplicada. Como colocamos a força para baixo o deslocamento do ponto C não se dá para baixo, mas sim, para cima.
Resposta
Exercício Resolvido #2
Elaboração própria
Supondo que o apoio A sofreu um recalque vertical para baixo de 10cm e pra esquerda de 5 cm, e o apoio B sofreu um recalque vertical para baixo de 1,5 cm, determine o deslocamento horizontal do ponto C do pórtico.
Passo 1
Sabemos que na teoria temos um passo a passo que devemos seguir, e vamos ver que fica bem mais tranquilo resolver o nosso problema.
A primeira coisa que devemos fazer é por uma carga unitária no ponto em que se deseja saber o deslocamento e na direção que se deseja conhecer o deslocamento. No nosso caso é no ponto C e horizontal, podendo ser pra esquerda ou pra direita.
Passo 2
Em seguida determinamos as reações de apoio devido a carga unitária
Passo 3
E esse passo é bem importante de se prestar atenção, pois desenhamos na estrutura a direção e o sentido dos recalques que foram apresentados no enunciado.
Passo 4
Agora precisamos ficar bem atentos, a nossa fórmula é
E como eu disse, precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,
e sempre que for no sentido contrário, será negativa.
Passo 5
Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
O menos significa que como colocamos a carga para direita, ela deveria ir para esquerda, ou seja, o deslocamento do ponto C não se dá para esquerda. Mas o sinal negativo indica que é para direita.
Resposta
Exercício Resolvido #3
Elaboração própria
Supondo que o apoio A sofreu um recalque vertical para baixo de 3cm, e o apoio B sofreu um recalque vertical para cima de 2 cm, determine o deslocamento vertical do ponto C do pórtico.
Passo 1
Sabemos que na teoria temos um passo a passo que devemos seguir, e vamos ver que fica bem mais tranquilo resolver o nosso problema.
A primeira coisa que devemos fazer é por uma carga unitária no ponto em que se deseja saber o deslocamento e na direção que se deseja conhecer o deslocamento. No nosso caso é no ponto C e vertical para baixo.
Passo 2
Em seguida determinamos as reações de apoio devido a carga unitária
Passo 3
E esse passo é bem importante de se prestar atenção, pois desenhamos na estrutura a direção e o sentido dos recalques que foram apresentados no enunciado.
Passo 4
Agora precisamos ficar bem atentos, a nossa fórmula é
E como eu disse, precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,
e sempre que for no sentido contrário, será negativa.
Passo 5
Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
O menos significa que como colocamos a carga para baixo, ela deveria subir, ou seja, o deslocamento do ponto C não se dá para baixo, mas sim, para cima.
Resposta
Exercício Resolvido #4
Elaboração própria
Supondo que o apoio A sofreu um recalque vertical para baixo de 1cm e pra esquerda de 1,4 cm, e o apoio C sofreu um recalque vertical para baixo de 3,2 cm, determine o deslocamento horizontal do ponto B da viga.
Passo 1
Sabemos que na teoria temos um passo a passo que devemos seguir, e vamos ver que fica bem mais tranquilo resolver o nosso problema.
A primeira coisa que devemos fazer é por uma carga unitária no ponto em que se deseja saber o deslocamento e na direção que se deseja conhecer o deslocamento. No nosso caso é no ponto B e vertical, podendo ser pra cima ou pra baixo.
Passo 2
Em seguida determinamos as reações de apoio devido a carga unitária
Passo 3
E esse passo é bem importante de se prestar atenção, pois desenhamos na estrutura a direção e o sentido dos recalques que foram apresentados no enunciado.
Passo 4
Agora precisamos ficar bem atentos, a nossa fórmula é
E como eu disse, precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,
e sempre que for no sentido contrário, será negativa.
Passo 5
Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
O sinal positivo indica que o sentido do vetor unitário escolhido foi correto, ou seja, para baixo.
Resposta
Exercício Resolvido #5
Elaboração própria
Uma viga possui as fibras da parte superior com uma temperatura de 25 °C e da parte inferior com 45 °C. sabendo disso determine o deslocamento vertical do ponto B. use:
Passo 1
Fala, pessoal!!! Tudo tranquilinho com vocês? Galera, tá na cara que essa questão é uma questão de deslocamento devido à temperatura não tá não? Então para resolvermos esse problema usamos a seguinte equação:
Lembrando que o problema quer o deslocamento vertical do ponto .
Como só existe uma barra de seção constante a gente pode utilizar a seguinte simplificação.
Além disso não existem a componente da normal então vamos ter:
Passo 2
Então vamos achar o diagrama de momento fletor devido à carga unitária. Lembrando que essa carga unitária deve ser posicionada no ponto em que queremos saber o deslocamento e na direção em que queremos saber o deslocamento (vertical). Dessa maneira teremos que:
Desenhando o diagrama teremos que:
E a área é dada por
Passo 3
Agora é substituir os termos na nossa fórmula
Substituindo teremos que:
Resposta
Exercício Resolvido #6
Elaboração própria
Uma viga possui as fibras da parte superior como uma temperatura de 20°C e da parte inferior com 50°c. sabendo disso determine o deslocamento vertical o ponto B. use:
Passo 1
sabemos que para calculo da temperatura usamos a seguinte equação:
Que podemos simplificar de acordo como o tipo de estrutura, no nosso caso como se trata de uma viga, podemos descartar a contribuição de normais, e ficar apenas com a contribuição de momentos fletores. Dessa maneira teremos que a nossa fórmula será.
Sabemos que a variação de temperatura, a altura e o coeficiente de dilatação térmicos são constantes na nossa equação, logo podemos escrever a mesma da seguinte maneira.
E sabemos que a integral do momento devido a carga unitária, integrado no comprimento S da barra, nada mais é que a área do diagrama, ou seja, nossa fórmula passa a ser.
Em que:
Passo 2
como podemos ver o que falta é exatamente o diagrama de momentos devido a carga unitária posicionada no ponto em que queremos saber o deslocamento, na direção em que queremos saber o deslocamento. Dessa maneira teremos que:
Desenhando o diagrama teremos que:
E a área dele é dada por
Passo 3
Agora é substituir os termos na nossa fórmula
Substituindo teremos que:
Resposta
Exercício Resolvido #7
Elaboração própria
Um pórtico possui as fibras da parte superior com uma temperatura de 60°C e da parte inferior com 20°c. sabendo disso determine o deslocamento vertical o ponto B. Use: Seção da viga de alma por cm de altura (viga retangular) e
Passo 1
Sabemos que para cálculo da temperatura usamos a seguinte equação:
Como trata-se de barras iguais vamos poder simplificar da seguinte forma:
Além disso, para esse caso não haverá momento fletor, logo podemos simplificar ainda mais:
Então a gente precisa basicamente achar os diagramas da normal para resolver essa questão.
Passo 2
Aplicando a força unitária vertical em vamos ter:
Desenhando o diagrama da normal para cada barra vamos ter:
Agora podemos calcular a área do diagrama lembrando que trata-se de uma compressão logo o termo será negativo:
Passo 3
Agora é substituir os termos na nossa fórmula. Aqui vale lembrar que temos uma seção retangular então o centroide da seção coincide com a temperatura média.
Substituindo teremos que:
Como o deslocamento deu negativo ele se dá no sentido inverso da carga unitária. Ou seja, o deslocamento será para cima.
Resposta
O deslocamento tem valor de para cima.
Exercício Resolvido #8
Elaboração própria
Uma treliça possui as fibras da parte superior com uma temperatura de 80°C e da parte inferior com 10°c. sabendo disso determine o deslocamento vertical o ponto E. use:
Passo 1
sabemos que para calculo da temperatura usamos a seguinte equação:
Que podemos simplificar de acordo como o tipo de estrutura, no nosso caso como se trata de uma treliça, podemos descartar a contribuição de momentos, e ficar apenas com a contribuição de normais. Dessa maneira teremos que a nossa fórmula será.
Sabemos que a temperatura no centro de gravidade da peça e o coeficiente de dilatação térmico são constantes na nossa fórmula, logo podemos escrever a mesma da seguinte maneira.
E sabemos que a integral do normal devido a carga unitária, integrado no comprimento S de cada uma das barras de treliça, nada mais é que a área do diagrama, ou seja, nossa fórmula passa a ser.
Em que:
Passo 2
como podemos ver o que falta é exatamente o diagrama de momentos devido a carga unitária posicionada no ponto em que queremos saber o deslocamento, na direção em que queremos saber o deslocamento. Dessa maneira teremos que:
Desenhando o diagrama de cada uma das barras teremos que:
Para o cálculo da área precisamos do comprimento de cada uma das barras, que podemos calcular por Pitágoras e com isso teremos que:
Agora calculamos o somatório das áreas (tome cuidado de manter os sinais):
Passo 3
Precisamos por fim determinar a temperatura no centro de gravidade da seção retangular. Sabemos que o centro de gravidade da seção retangular é no meio da seção, sendo assim a temperatura será dada por:
Logo a temperatura no centro de gravidade da seção é de 45°C
Passo 4
Agora é substituir os termos na nossa fórmula
Substituindo teremos que:
Vale lembrar que colocamos nossa carga unitária para baixo contando da estrutura deformar para baixo, porém podemos ver que a deformação deu negativa, logo, a estrutura deforma na outra direção, ou seja, pra cima.