Graus de Hiperestaticidade
Produzido por Pablo RicardoTeoria
Introdução
Até aqui aprendemos como trabalhar com uma estrutura do tipo isostática, porém a partir daqui iremos aprender como trabalhar com estruturas do tipo Hiperestáticas, para isso precisamos aprender alguns conceitos importantes antes de partirmos para o principal, e esse é o objetivo dessa aula.
Hiperestaticidade externa
Sabemos que uma estrutura sempre vai ser composta por incógnitas e equações. As equações são bem simples, e sabemos que temos duas formas de obter o número de equações. O primeiro são as três equações de equilíbrio que já conhecemos bem.
E o segundo está ligado as rótulas, em que o número de equações que podemos obter de uma rótula, é sempre o número de barras que chegam na rótula, menos 1. Ou seja, no exemplinho abaixo podemos ver como sempre saber quantas equações podemos ganhar com uma rótula.
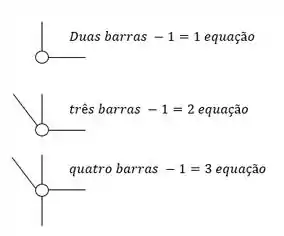
Já o número de incógnitas podemos obter pelos apoios da nossa estrutura seguindo a regrinha:

Ou seja, com o nosso exemplo aqui de baixo conseguimos determinar quantos hiperestáticos a nossa estrutura tem:
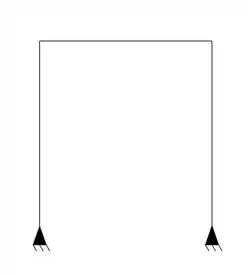
Percebemos que nossa estrutura não possui rotulas, logo só possui as 3 equações de equilíbrio que deveria ter. da mesma maneira vemos que ele possui dois apoios do segundo gênero, com isso, podemos dizer que possui 4 incógnitas, então para determinar o número de hiperestáticos basta fazer:
Hiperestaticidade interna
Esse é mais fácil de ser observado, pois sempre aparecerá em ponto em que a estrutura se fecha fazendo uma estrutura em que não é simples determinar os esforços internos. Sempre que isso acontecer, nós teremos 3 incógnitas de esforço interno, por região fechada, por exemplo:
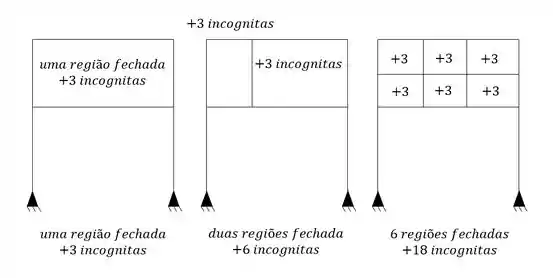
E assim determinamos o número de hiperestáticos internos pela fórmula:
Total de hiperestáticos de uma estrutura
Nada mais é que a soma do número de hiperestáticos externos com o número de hiperestáticos internos, por exemplo:
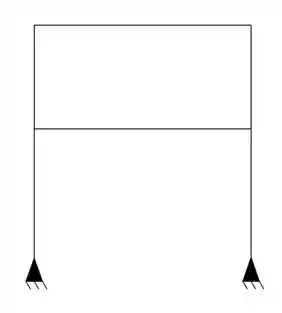
- Hiperestáticos externos
- Hiperestáticos interno
- Hiperestáticos totais
- Hiperestáticos externos
- Temos 2 apoios do terceiro gênero, logo, temos 6 incógnitas no total.
- Temos 3 equações de equilíbrio, e na nossa rótula chegam 3 barras, logo, temos um total de +2 equações, totalizando 5 equações. Com isso temos:
- Hiperestáticos interno
- Podemos ver que temos um total de 1 região fechada, logo
- Hiperestáticos totais
- Hiperestáticos totais pelo macete
- Sabemos que temos 2 apoios do terceiro gênero, totalizando 6 incógnitas externas
- Temos 1 região fechada, totalizando 3 incógnitas internas
- Temos 3 equações de equilíbrio
- Temos uma rótula com 3 barras que vai nós dar mais 2 equações
Macete para determinar o número de hiperestáticos totais de uma estrutura
É bem simples o macete, é basicamente somar todos os números de incógnitas, sejam elas externas e internas, e subtrair o número de equações, sejam elas as 3 de equilíbrio ou que venham de rótulas. Com isso temos a seguinte fórmula.
Usando o nosso exemplo anterior temos que:
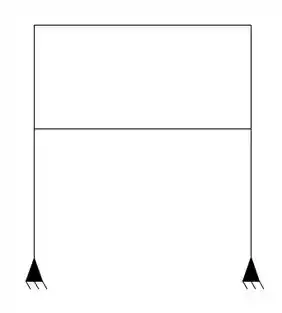
Exemplo 2
Determine o total de hiperestáticos da estrutura abaixo:
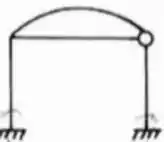
Agora que você já viu que não é um bicho de sete cabeças determinar o número de hiperestáticos de uma estrutura, bora fazer mais alguns exercícios, e partir para o método das forças em que vamos precisar saber muito bem como funcionam os hiperestáticos, partiu? Vamos lá então 😊.