Grupo de incógnitas em estruturas simétricas
Produzido por Pablo RicardoTeoria
Determinando o sistema isostático
Assim como o artificio de arranjo de cargas em estruturas simétricas, o arranjo de incógnitas tem o intuito de facilitar os cálculos também, mas nesse caso, ao invés de manipular as cargas, o artificio irá manipular as incógnitas.
No nosso arranjo de incógnitas, nós iremos pegar a nossa estrutura hiperestática e iremos quebrar os seus vínculos, com isso iremos ter a nossa estrutura isostática, juntamente com as incógnitas dela, que nesse caso serão os hiperestáticos. Vamos ver um exemplo que fica mais fácil de ser observado.
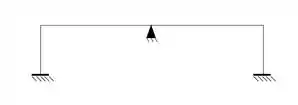
Perceba que temos dois apoios do terceiro gênero, um do segundo gênero, totalizando 8 incógnitas. Como temos 3 equações de equilíbrio, não tendo nenhuma rótula e nenhuma região fechada, teremos ao todo 5 hiperestáticos, que são as nossas 5 incógnitas.
E agora que vem o pulo do gato. Para usarmos o nosso artifício de incógnitas, precisamos quebrar as rótulas simetricamente (no futuro vamos ver que na verdade precisamos apenas garantir que o sistema de incógnitas seja simétrico, e não em si a quebra dos vínculos, mas de início, sempre que fizermos a quebra de vínculos simetricamente, o sistema de incógnitas também será).
Fazendo isso teremos que:
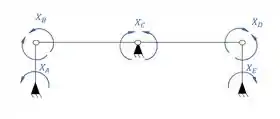
E perceba que sempre que quebrarmos um vínculo, colocando uma rótula, deveremos colocar a incógnita em ambos os lados da rótula, como por exemplo e . Outra coisa que você deve perceber é que as quebras que eu fiz foram simétricas, ou seja, sempre foi feito uma quebra correspondente usando o eixo de simetria da estrutura como referência.
O método dos arranjos de incógnitas
O método em si tem o objetivo de anular o máximo de fatores da nossa matriz de deslocamentos. Como assim? Veja o seguinte, imagine que pudéssemos escrever o nosso grupo de incógnitas como dois sistemas, um colocando esse grupo de incógnitas como um sistema simétrico de incógnitas, e outro como um sistema assimétrico, assim teríamos.
- Sistemas simétrico
- Sistemas para a parte simétrica
- Sistemas para a parte assimétrica
- Macete 1
- Macete 2
- Macete 3
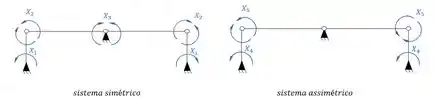
E perceba que não temos o correspondente porque o assimétrico dele anularia a si mesmo.
E agora que surge o nome do método, porque o nome é grupo de incógnitas? Porque agora eu posso dizer que o nosso sistema inicial isostático, pode ser escrito em função dos sistemas simétricos e assimétricos da seguinte maneira.
E bem, até aqui está tudo muito bonito, mas a pergunta que você tem que se fazer agora é, como determinamos os valores de ?
Calculando a matriz de rigidez
É agora que vem o segundo pulo do gato, e para isso, vamos observar cada diagrama, de cada sistema, referente a cada incógnita.
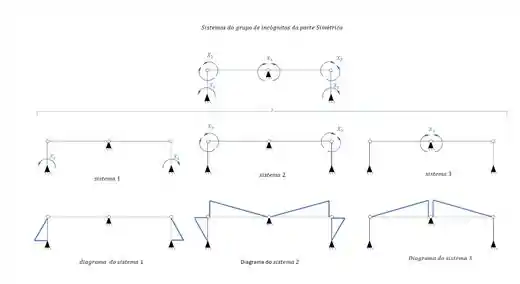
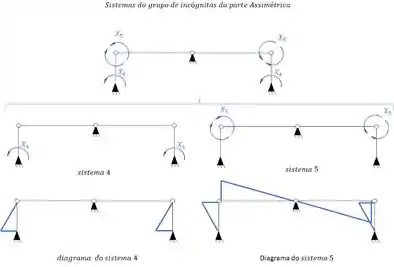
Combinação dos sistemas
O único sistema que não aparece ali em cima são os sistemas . Isso significa que eles não existam? Não, eles só não apareceram porque eles não tem relevância para entendimento do grupo de incógnitas, ou seja, são calculados da maneira que já sabemos, ou seja, combinando o sistema zero, que é o diagrama do sistema isostático com o carregamento atuante, com o diagrama do sistema isostático do hiperestático relativo ao cálculo. E agora vem o terceiro e último pulo do gato, e que para mim é o pulo mais importante. Sabemos que para determinar o nosso sistema de incógnitas precisamos combinar os sistemas, e o macete é o seguinte.
Sempre que combinarmos os diagramas referentes ao sistema simétrico, esses valores serão diferentes de zero, ou seja, no nosso exemplo temos os seguintes diagramas referentes a parte simétrica.

Ou seja, se combinarmos eles entre si obteremos as seguintes deformações do nosso sistema ()
Sempre que combinarmos os diagramas referentes ao sistema Assimétrico, esses valores serão diferentes de zero, ou seja, no nosso exemplo temos os seguintes diagramas referentes a parte assimétrica.
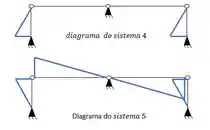
Ou seja, se combinarmos eles entre si obteremos as seguintes deformações do nosso sistema (
Esse é o macete mais importante que temos, pois sempre que combinarmos os diagramas do sistema simétrico, com os diagramas do sistema assimétrico, ou seja, os 5 diagramas, juntando um com relação ao outro, SEMPRE, a deformação será zero.
Isso é fácil de visualizar, pois perceba, no sistema simétrico, todos os valores dão positivo ou negativo, enquanto que no sistema assimétrico, metade dos valores são positivos, e a outra metade é negativa, ou seja, quando combinarmos os dois sistemas, a metade positiva vai anular a metade negativa, e por isso, SEMPRE, teremos essa combinação dando zero.
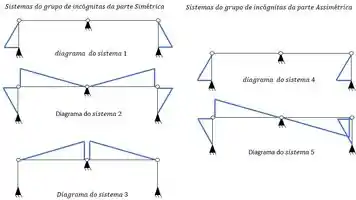
Ou seja, no nosso exemplo as deformações que irão zerar são (
O sistema final
Sabemos que o nosso sistema, em um caso de 5 hiperestáticos, é dado por:
Isolando os termos sem incógnitas
E agora vamos substituir tudo que tem zero no nosso sistema
Escrevendo na forma de matriz teremos que
E assim conseguimos resolver o nosso problema tendo 12 zeros na nossa equação. Ou seja, conseguimos transformar uma matriz 5X5, muito complexa de resolver, em uma matriz cheia de zeros, com uma parte de uma pequena matriz 3X3 e uma outra de 2X2, facilitando e muito os cálculos.
Diagramas
Perceba que no nosso problema todos os hiperestáticos são momentos fletores, e lembre-se que eles na verdade foram a separação de um sistema inicial, ou seja, se quiséssemos o diagrama de momentos, tendo todos os momentos calculados, bastaria fazer a equação que achamos bem no início dessa aula.
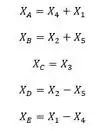
Em que o “X” com índice de letra é o valor real, e o “X” com índice de numero é o valor achado na solução do sistema.
Mas e se não tivesse pedindo os momentos? Ai bastaria usar a fórmula que já conhecemos, que é dada por.

E essa equação pode ser usado para qualquer esforço (cortante, normal, momento, reação de apoio) assim como para qualquer ponto (A,B,C,D,E). Por exemplo, se quisermos saber o momento fletor real no ponto A, nossa equação será.
O método dos arranjos de incógnitas
Calculando a matriz de rigidez
Combinação dos sistemas
O sistema final
Diagramas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine a estrutura dividida com o arranjo de incógnitas simétricos e assimétricos, e determine a relação necessária para o cálculo dos esforços reais.

Passo 1
Fala, pessoal!!! Essa questão aqui é boa para trabalhar o conceito de grupo de incógnitas em estruturas simétricas porque é uma das formas mais simples que isso pode ficar.
Para resolver essa questão a gente só precisa quebrar os vínculos nos lugares corretos e achar os respectivos sistemas e equações. Então vamos lá?
Passo 2
Primeiro temos que definir o número de hiperestáticos da nossa estrutura.
- Sabemos que temos 3 apoios do segundo gênero
- Ao todo então temos 6 incógnitas no nosso problema
- Como não tem nenhuma rótula, temos no total 3 equações de equilíbrio
- Logo fazendo a continha:
Logo precisamos quebrar apenas 3 vínculo, simetricamente. Essa quebra vai ser o da seguinte maneira.
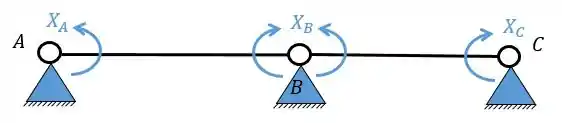
Passo 3
Agora precisamos dividir os sistemas simétricos e assimétricos, em que teremos a seguinte divisão.
- Sistema simétrico
- Sistema assimétrico
- Sistemas de relação entre o grupo de incógnitas
- Sistema simétrico
- Sistema Assimétrico
- Sistema de equações
- Grupo de incógnitas
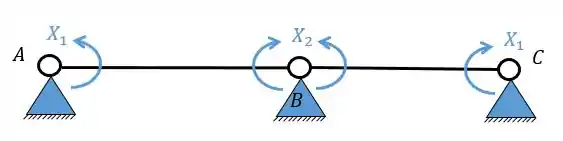
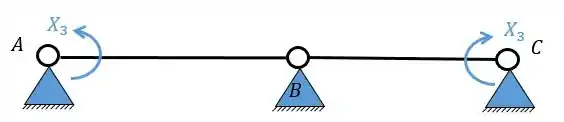
Passo 4
Por fim, precisamos apenas dividir os sistemas que precisamos desenhar os diagramas.

Agora a gente tem que perceber algumas coisas: os sistemas simétricos (1 e 2) irão gerar as deformações relativas entre si ( e ).
Enquanto os sistemas assimétricos também geram deformações relativas entre si, no caso apenas .
Passo 5
Agora antes de montar a matriz a gente tem que lembrar que a combinação de sistemas simétricos com assimétricos é sempre nula! Logo, vamos ter:
Montando o sistema teremos que ele será da seguinte maneira:
E assim resolvemos os objetivos do nosso exercício.
Resposta
Sistemas criados e sua simetria ou assimetria
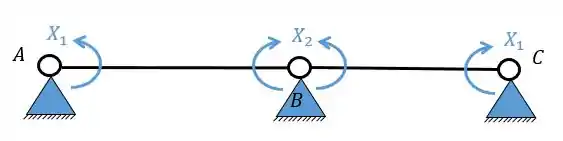
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Origem do Exercício
Determine a estrutura dividida com o arranjo de incógnitas simétricos e assimétricos, e determine a relação necessário para o cálculo dos esforços reais.

Passo 1
Primeiro temos que definir o número de hiperestáticos da nossa estrutura.
- Sabemos que temos 1 apoio do segundo gênero
- E 4 apoios do primeiro gênero
- Ao todo então temos 6 incógnitas no nosso problema
- Como não tem nenhuma rótula, temos no total 3 equações de equilíbrio
- Logo fazendo a continha:
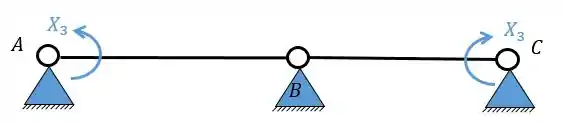
Logo precisamos quebrar 3 vínculos, simetricamente. Essa quebra vai ser o da seguinte maneira.
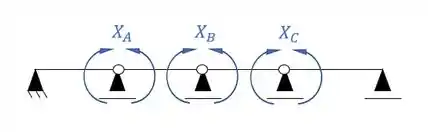
Passo 2
Agora precisamos dividir os sistemas simétricos e assimétricos, em que teremos a seguinte divisão.
- Sistema simétrico
- Sistema assimétrico
- Sistemas de relação entre o grupo de incógnitas
- Sistema simétrico
- Sistema Assimétrico
- Sistema de equações
- Grupo de incógnitas
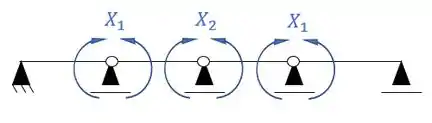
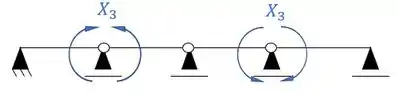
Passo 3
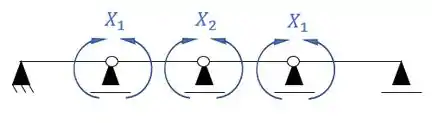
Por fim, precisamos apenas dividir os sistemas que precisamos desenhar os diagramas.
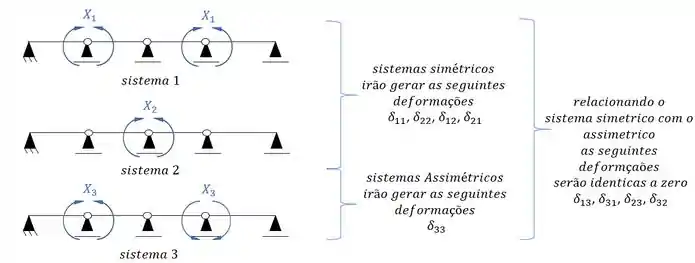
Montando o sistema teremos que ele será da seguinte maneira:
E assim resolvemos os objetivos do nosso exercício.
Resposta
Sistemas criados e sua simetria ou assimetria
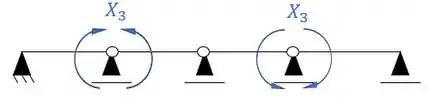
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Origem do Exercício
Determine a estrutura dividida com o arranjo de incógnitas simétricos e assimétricos, e determine a relação necessário para o cálculo dos esforços reais.
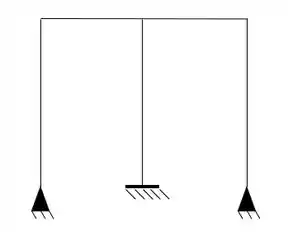
Passo 1
Primeiro temos que definir o número de hiperestáticos da nossa estrutura.
- Sabemos que temos 2 apoios do segundo gênero
- E 1 apoio do terceiro gênero
- Ao todo então temos 7 incógnitas no nosso problema
- Como não tem nenhuma rótula, temos no total 3 equações de equilíbrio
- Logo fazendo a continha:
Logo precisamos quebrar 4 vínculos, simetricamente. Essa quebra vai ser o da seguinte maneira.
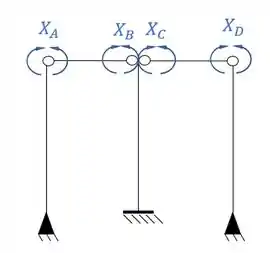
Passo 2
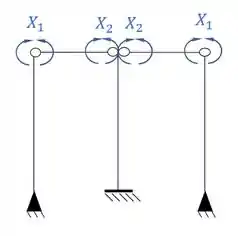
Agora precisamos dividir os sistemas simétricos e assimétricos, em que teremos a seguinte divisão.
- Sistema simétrico
- Sistema assimétrico
- Sistemas de relação entre o grupo de incógnitas
- Sistema simétrico
- Sistema Assimétrico
- Sistema de equações
- Grupo de incógnitas
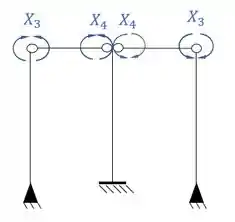
Passo 3
Por fim, precisamos apenas dividir os sistemas que precisamos desenhar os diagramas.
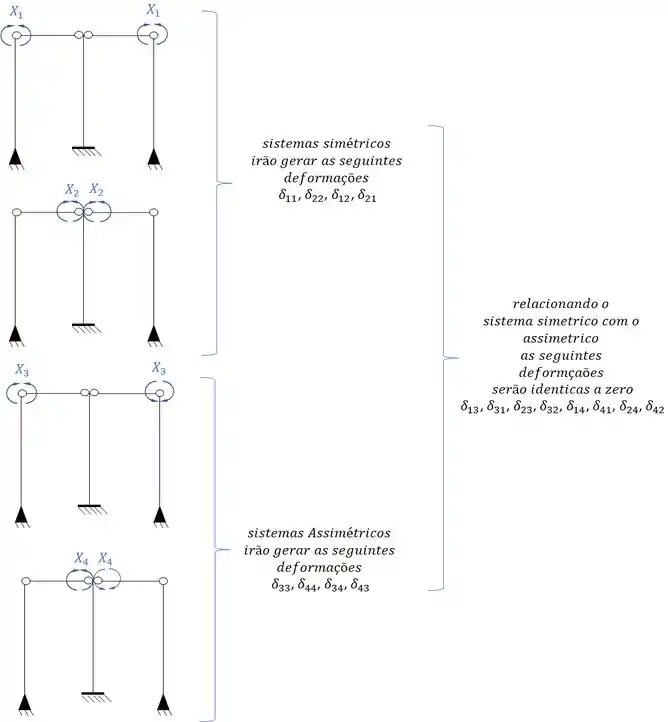
Montando o sistema teremos que ele será da seguinte maneira:
E assim resolvemos os objetivos do nosso exercício.
Resposta
Sistemas criados e sua simetria ou assimetria
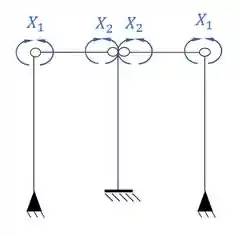
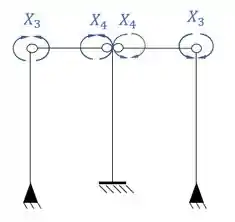
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
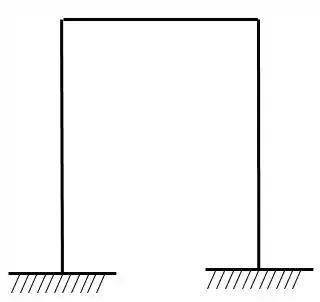
Determine a estrutura dividida com o arranjo de incógnitas simétricos e assimétricos, e determine a relação necessária para o cálculo dos esforços reais.
Passo 1
Fala, pessoal!!! Essa questão aqui é boa para trabalhar o conceito de grupo de incógnitas em estruturas simétricas porque é uma das formas mais simples que isso pode ficar.
Para resolver essa questão a gente só precisa quebrar os vínculos nos lugares corretos e achar os respectivos sistemas e equações. Então vamos lá?
Passo 2
Primeiro temos que definir o número de hiperestáticos da nossa estrutura.
- Sabemos que temos 2 apoios do terceiro gênero
- Ao todo então temos 6 incógnitas no nosso problema
- Como não tem nenhuma rótula, temos no total 3 equações de equilíbrio
- Logo fazendo a continha:
Logo precisamos quebrar 3 vínculos, simetricamente. Essa quebra vai ser o da seguinte maneira.
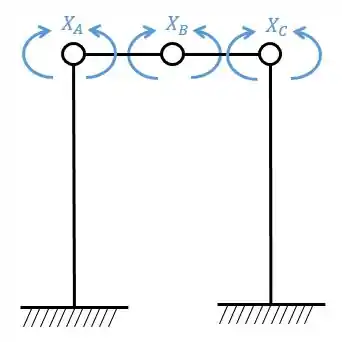
Passo 3
Agora precisamos dividir os sistemas simétricos e assimétricos, em que teremos a seguinte divisão.
- Sistema simétrico
- Sistema assimétrico
- Sistemas de relação entre o grupo de incógnitas
- Sistema simétrico
- Sistema Assimétrico
- Sistema de equações
- Grupo de incógnitas
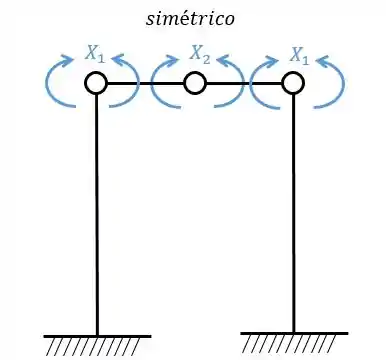
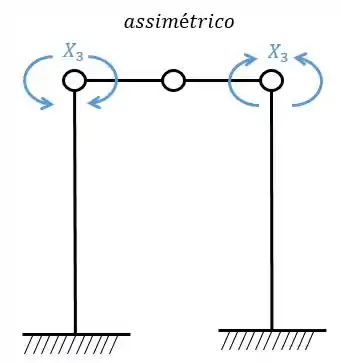
Passo 4
Por fim, precisamos apenas dividir os sistemas que precisamos desenhar os diagramas.
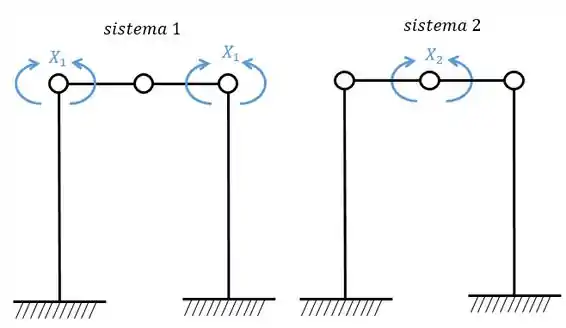
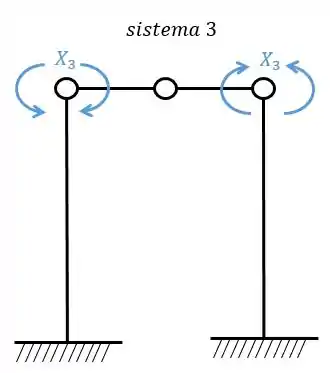
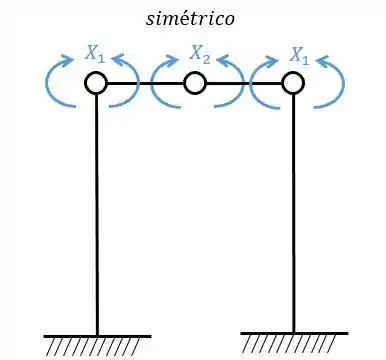
Agora a gente tem que perceber algumas coisas: os sistemas simétricos (1 e 2) irão gerar as deformações relativas entre si.
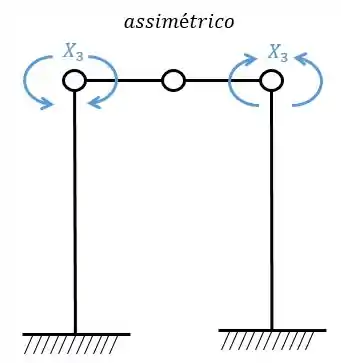
Enquanto os sistemas assimétricos (3) também geram deformações relativas entre si, no caso apenas.
Passo 5
Agora antes de montar a matriz a gente tem que lembrar que a combinação de sistemas simétricos com assimétricos é sempre nula! Logo, vamos ter para os sistemas simétricos:
Para os sistema assimétricos:
Repare que poderíamos colocar como uma matriz se quiséssemos =D
Resposta
Sistemas criados e sua simetria ou assimetria
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Origem do Exercício
Determine a estrutura dividida com o arranjo de incógnitas simétricos e assimétricos, e determine a relação necessário para o cálculo dos esforços reais.

Passo 1
Primeiro temos que definir o número de hiperestáticos da nossa estrutura.
- Sabemos que temos 1 apoio do segundo gênero
- E 1 apoio do primeiro gênero
- E temos uma região fechada que nós da mais 3 incógnitas
- Ao todo então temos 6 incógnitas no nosso problema
- Como não tem nenhuma rótula, temos no total 3 equações de equilíbrio
- Logo fazendo a continha:
Logo precisamos quebrar 3 vínculos, simetricamente. Essa quebra vai ser o da seguinte maneira.

Passo 2
Agora precisamos dividir os sistemas simétricos e assimétricos, em que teremos a seguinte divisão.
- Sistema simétrico
- Sistema assimétrico
- Sistemas de relação entre o grupo de incógnitas
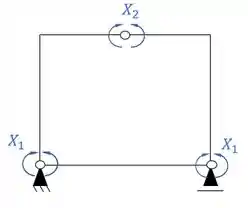
- Sistema simétrico
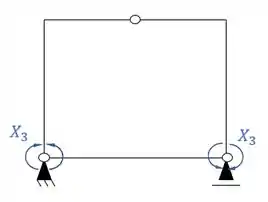
- Sistema Assimétrico
- Sistema de equações
- Grupo de incógnitas
Passo 3
Por fim, precisamos apenas dividir os sistemas que precisamos desenhar os diagramas.
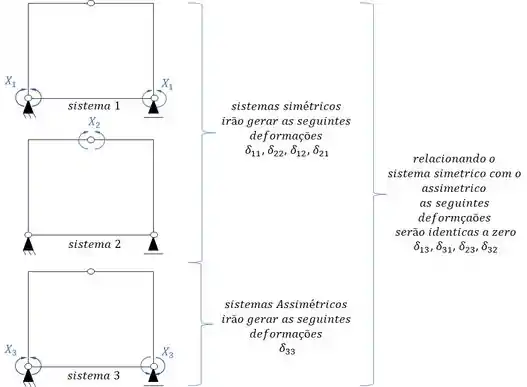
Montando o sistema teremos que ele será da seguinte maneira:
E assim resolvemos os objetivos do nosso exercício.
Resposta
Sistemas criados e sua simetria ou assimetria
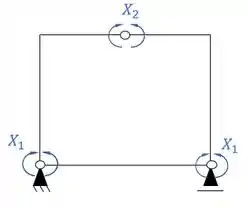
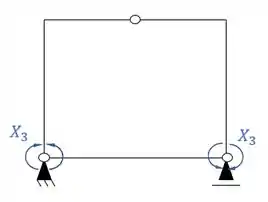
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Origem do Exercício
Determine a estrutura dividida com o arranjo de incógnitas simétricos e assimétricos, e determine a relação necessário para o cálculo dos esforços reais.
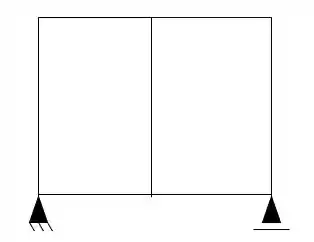
Passo 1
Primeiro temos que definir o número de hiperestáticos da nossa estrutura.
- Sabemos que temos 1 apoio do segundo gênero
- E 1 apoio do primeiro gênero
- E temos duas regiões fechadas que nós da mais 6 incógnitas
- Ao todo então temos 9 incógnitas no nosso problema
- Como não tem nenhuma rótula, temos no total 3 equações de equilíbrio
- Logo fazendo a continha:
Logo precisamos quebrar 6 vínculos, simetricamente. Essa quebra vai ser o da seguinte maneira.
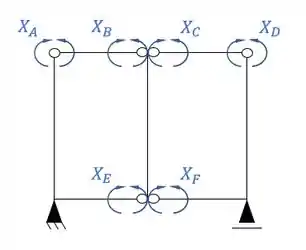
Passo 2
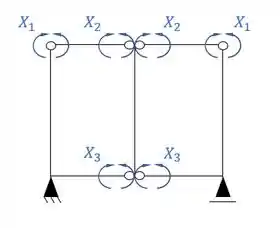
Agora precisamos dividir os sistemas simétricos e assimétricos, em que teremos a seguinte divisão.
- Sistema simétrico
- Sistema assimétrico
- Sistemas de relação entre o grupo de incógnitas
- Sistema simétrico
- Sistema Assimétrico
- Sistema de equações
- Grupo de incógnitas
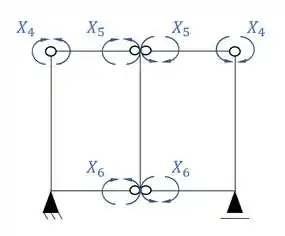
Passo 3
Por fim, precisamos apenas dividir os sistemas que precisamos desenhar os diagramas.
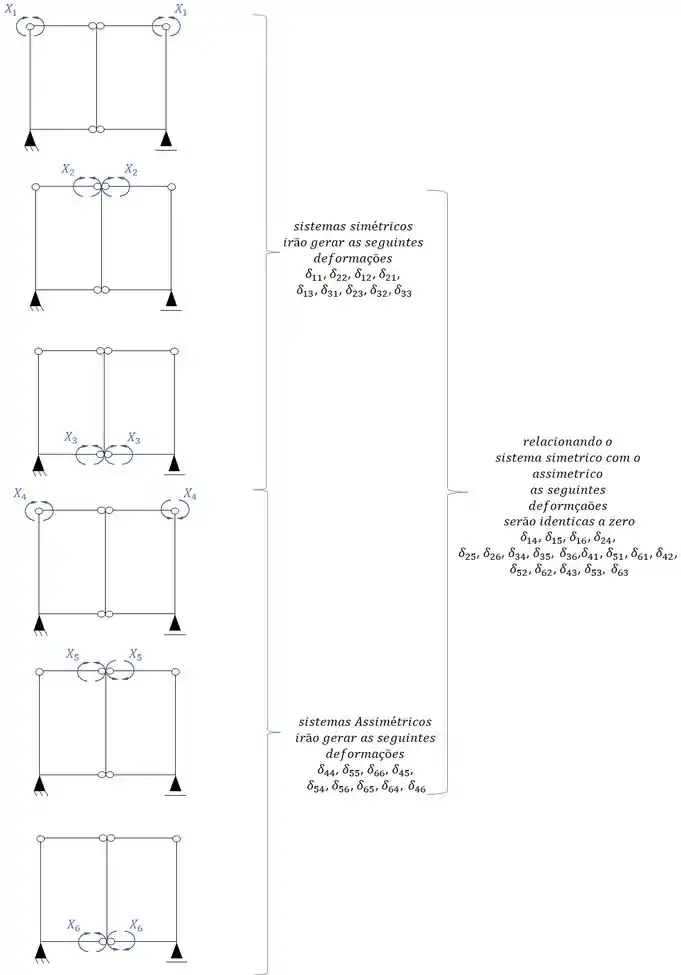
Montando o sistema teremos que ele será da seguinte maneira:
E assim resolvemos os objetivos do nosso exercício.
Resposta
Sistemas criados e sua simetria ou assimetria
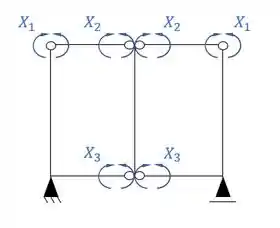
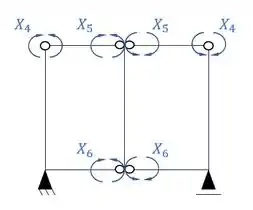
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Origem do Exercício
Determine a estrutura dividida com o arranjo de incógnitas simétricos e assimétricos, e determine a relação necessário para o cálculo dos esforços reais.
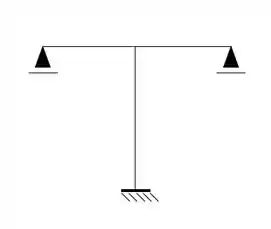
Passo 1
Primeiro temos que definir o número de hiperestáticos da nossa estrutura.
- Sabemos que temos 2 apoios do primeiro gênero
- E 1 apoio do segundo gênero
- Ao todo então temos 5 incógnitas no nosso problema
- Como não tem nenhuma rótula, temos no total 3 equações de equilíbrio
- Logo fazendo a continha:
Logo precisamos quebrar 2 vínculos, simetricamente. Essa quebra vai ser o da seguinte maneira.
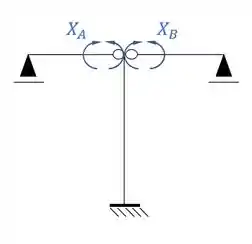
Passo 2
Agora precisamos dividir os sistemas simétricos e assimétricos, em que teremos a seguinte divisão.
- Sistema simétrico
- Sistema assimétrico
- Sistemas de relação entre o grupo de incógnitas
- Sistema simétrico
- Sistema Assimétrico
- Sistema de equações
- Grupo de incógnitas
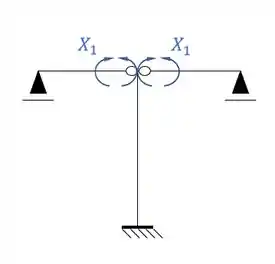
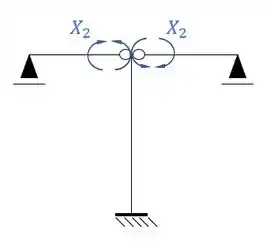
Passo 3
Por fim, precisamos apenas dividir os sistemas que precisamos desenhar os diagramas.
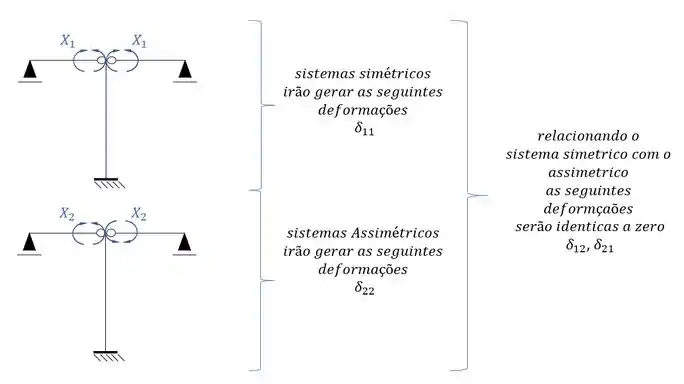
Montando o sistema teremos que ele será da seguinte maneira:
E assim resolvemos os objetivos do nosso exercício.
Resposta
Sistemas criados e sua simetria ou assimetria
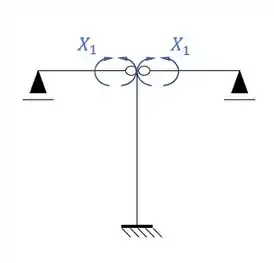
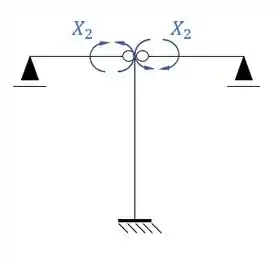
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Elaboração própria
Determine a estrutura dividida com o arranjo de incógnitas simétricos e assimétricos, e determine a relação necessária para o cálculo dos esforços reais.
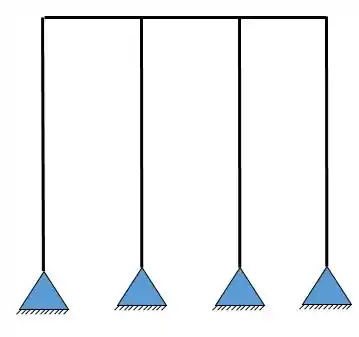
Passo 1
Fala, pessoal!!! Essa questão aqui é boa para trabalhar o conceito de grupo de incógnitas em estruturas simétricas porque é uma das formas mais simples que isso pode ficar.
Para resolver essa questão a gente só precisa quebrar os vínculos nos lugares corretos e achar os respectivos sistemas e equações. Então vamos lá?
Passo 2
Primeiro temos que definir o número de hiperestáticos da nossa estrutura.
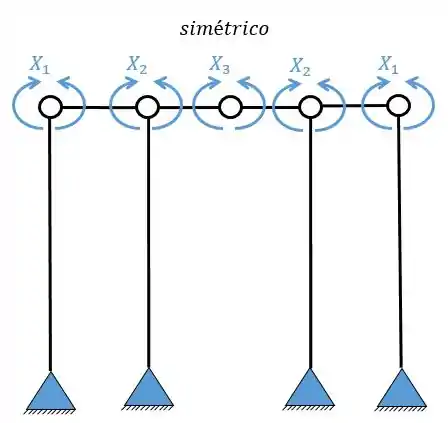
- Sabemos que temos 4 apoios do segundo gênero
- Ao todo então temos 8 incógnitas no nosso problema
- Como não tem nenhuma rótula, temos no total 3 equações de equilíbrio
- Logo fazendo a continha:
Logo precisamos quebrar 5 vínculos, simetricamente. Essa quebra vai ser o da seguinte maneira.
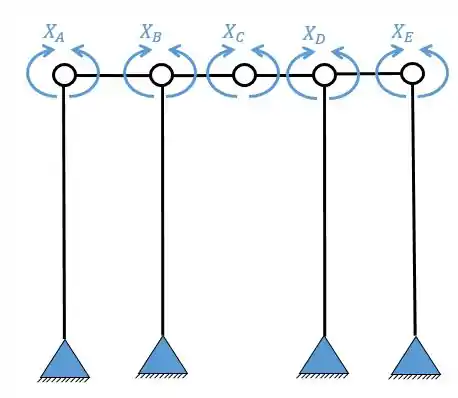
Passo 3
Agora precisamos dividir os sistemas simétricos e assimétricos, em que teremos a seguinte divisão.
- Sistema simétrico
- Sistema assimétrico
- Sistemas de relação entre o grupo de incógnitas
- Sistema simétrico
- Sistema Assimétrico
- Sistema de equações
- Grupo de incógnitas
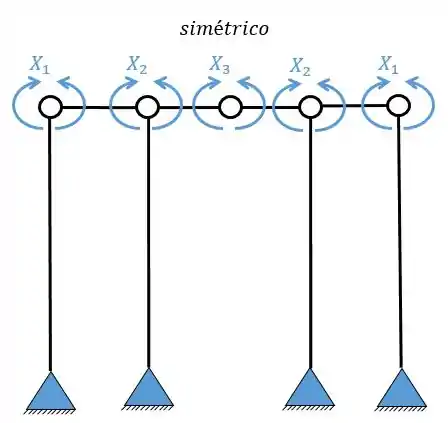
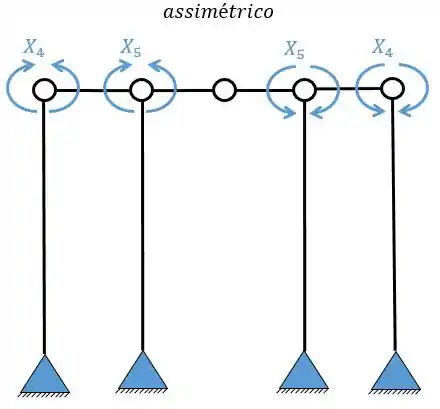
Passo 4
Por fim, precisamos apenas dividir os sistemas que precisamos desenhar os diagramas.
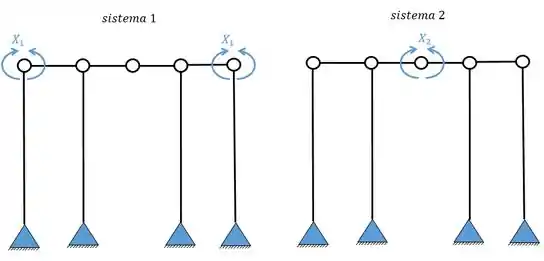
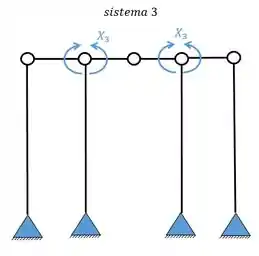
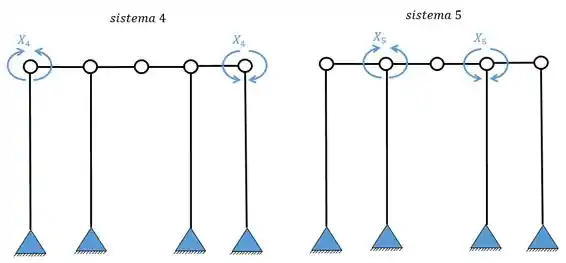
Agora a gente tem que perceber algumas coisas: os sistemas simétricos (1, 2 e 3) irão gerar as deformações relativas entre si.
Enquanto os sistemas assimétricos (4 e 5) também geram deformações relativas entre si, no caso apenas.
Passo 5
Agora antes de montar a matriz a gente tem que lembrar que a combinação de sistemas simétricos com assimétricos é sempre nula! Logo, vamos ter para os sistemas simétricos:
Para os sistema assimétricos:
Repare que poderíamos colocar como uma matriz se quiséssemos =D
Resposta
Sistemas criados e sua simetria ou assimetria

Resposta
Ei, a resposta está no passo a passo :)