Arranjo de cargas em Estruturas Simétricas
Produzido por Pablo RicardoTeoria
O artificio de cargas
Pessoal, imaginem que a gente tem o problema abaixo e queremos descobrir as forças de reação nos apoios.

Vou ensinar para vocês um método bem legal de resolver esse tipo de questão. Nós vamos trocar uma estrutura muito complexa, por duas estruturas de fácil solução.
O primeiro pré-requisito, é ser um pórtico simétrico. Então sempre garanta que você estará fazendo isso em UMA ESTRUTURA SIMETRICA.
Perceba que poderíamos reescrever a nossa estrutura, que percebe, possui 3 hiperestáticos da seguinte maneira.
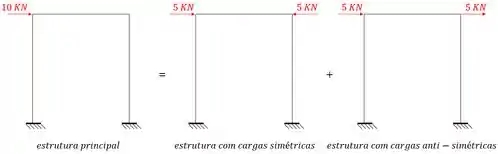
Perceba que ao somarmos a estrutura com cargas simétricas, e a estrutura com cargas antissimétricas, obtemos exatamente a nossa estrutura principal inicial. Mas como eu disse, porque faríamos essa troca?
A vantagem do uso do artifício (cortando apenas pontos)
Para sabermos as vantagens, precisamos aprender uma regrinha. E essa regrinha se divide da seguinte maneira.
- Se passarmos uma faca cortando o eixo de simetria da nossa estrutura, e essa faca cortar apenas pontos, ou seja, nunca cortar uma barra por todo o seu comprimento, trocaremos metade da estrutura por:
- Na estrutura com carga simétrica (colocaremos um carrinho)
- Na estrutura com carga anti-simétrica (colocaremos um apoio do primeiro gênero)
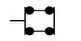
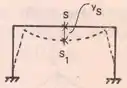
E fazemos isso porque se olharmos como a estrutura deforma, vemos que ela apenas se deforma verticalmente no eixo de simetria, ou seja, o movimento só é liberado na vertical, por isso usamos o carrinho. Ou seja, podemos dizer que nossa estrutura tem deslocamento horizontal e rotação nulas, e o esforço que é nulo nesse caso é o cortante, sendo normal e momento não nulos.
Dessa maneira podemos reescrever o nosso pórtico como:
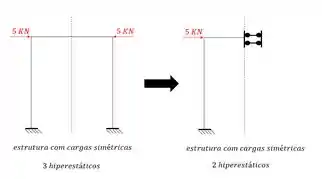
Observe que tínhamos uma estrutura com 3 hiperestáticos inteiro a ser resolvido. E agora passaríamos a ter metade da estrutura e ainda com 1 hiperestático a menos.
E perceba que mesmo que fossem várias barras, se cortássemos em apenas um ponto, trocaríamos tudo pelo apoio de carrinho.
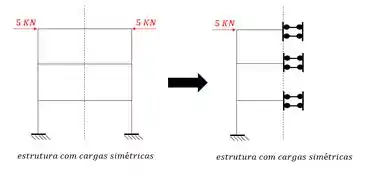
- Se passarmos uma faca cortando o eixo de simetria da nossa estrutura, e essa faca cortar uma barra por todo o seu comprimento, trocaremos metade da estrutura por:
- Na estrutura com carga simétrica (colocaremos um engaste)
- Na estrutura com carga anti-simétrica (manteremos a barra cortada, porém usaremos ela com metade do valor da inércia dela)

E fazemos isso porque se olharmos como a estrutura deforma, vemos que ela não permite deformações no eixo de simetria, ou seja, o movimento não é liberado em nenhuma direção. Ou seja, podemos dizer que nossa estrutura não tem deslocamento horizontal, vertical e nem rotação, e com isso possui todos os esforços (normais, momentos e cortantes)
Dessa maneira podemos reescrever o nosso pórtico como:
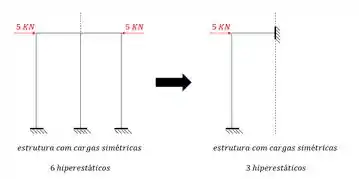
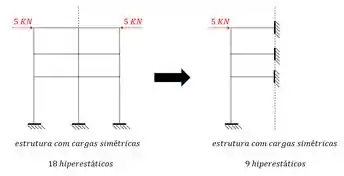
Observe que tínhamos uma estrutura com 6 hiperestáticos inteiro a ser resolvido. E agora passaríamos a ter metade da estrutura e ainda com metade do número de hiperestáticos.
E perceba que mesmo que fossem várias barras, se cortarmos por todo o comprimento, iremos trocar toda a metade por apoios de engaste.
- Diagrama da Estrutura com cargas simétricas
- Diagrama da Estrutura com cargas anti-simétricas
- Diagrama final

E fazemos isso porque se olharmos como a estrutura deforma, vemos que ela rotaciona em torno do eixo de simetria, dessa maneira podemos dizer que a estrutura irá se comportar como evitando o movimento vertical, e permitindo a tendência de movimento horizontal e rotação. Ou seja, podemos dizer que nossa estrutura tem deslocamento vertical nulo, e o esforços que são nulos nesse caso são o normal e o momento fletor, sendo apenas o cortante não nulos.
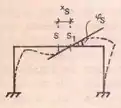
Dessa maneira podemos reescrever o nosso pórtico como:
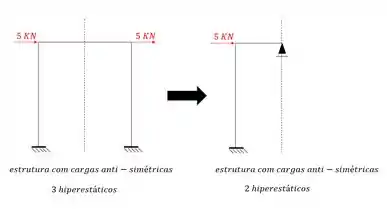
Observe que tínhamos uma estrutura com 3 hiperestáticos inteiro a ser resolvido. E agora passaríamos a ter metade da estrutura e ainda com 2 hiperestático a menos.
E perceba que mesmo que fossem várias barras, se cortássemos em apenas um ponto, trocaríamos tudo pelo apoio do primeiro gênero.
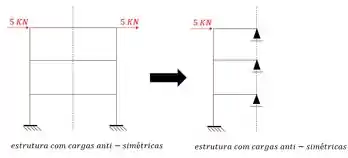
A vantagem do uso do artifício (cortando apenas barras)
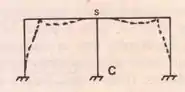
Nesse caos a nossa estrutura vai ter uma barra exatamente no eixo de simetria como podemos ver aqui em baixo.
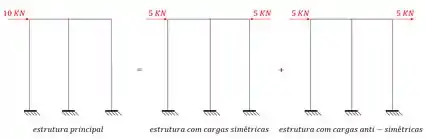
![]()
Nesse caso a barra irá deformar junto com a estrutura, mas ainda sim mantendo as suas restrições. De maneira artificial consideramos a barra com metade da inércia porque lembre-se que estaremos descartando metade da estrutura, então considerar metade da inércia no eixo de simetria permite termos valores mais próximos da realidade.
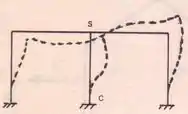
Dessa maneira podemos reescrever o nosso pórtico como:
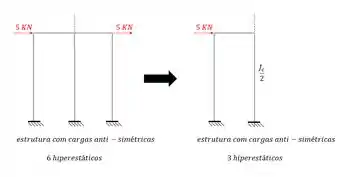
Observe que tínhamos uma estrutura com 6 hiperestáticos inteiro a ser resolvido. E agora passaríamos a ter metade da estrutura e ainda com metade do número de hiperestáticos
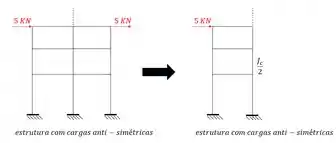
E perceba que mesmo que fossem várias barras, se cortássemos todo o comprimento da barra, trocaríamos tudo pela nossa barra com metade da inércia.
Os diagramas
Os diagramas são bem simples de se pegar o jeito, e vou fazer um exemplo fictício pra ficar bem fácil de pegar.
Você vai estar lá, felizão que calculou metade da estrutura, como fazer para a outra metade da estrutura? Para isso é só seguir o seguinte esquema:
Tendo metade do diagrama devemos fazer o seguinte.
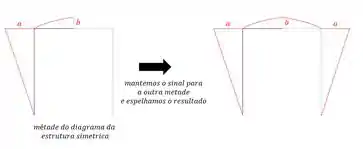
Perceba que quando falo manter o sinal é porque se “a” é positivo de um lado ele será positivo do outro na estrutura simétrica também. E isso vale para todos os esforços, sejam ele normal, momento fletor ou cortante.
Tendo metade do diagrama devemos fazer o seguinte.
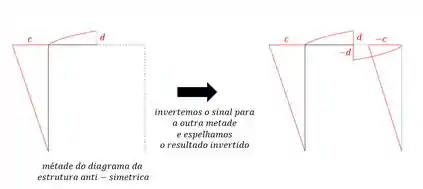
Perceba que quando falo inverter o sinal é porque se “c” é positivo de um lado ele será negativo do outro na estrutura anti-simétrica. E isso vale para todos os esforços, sejam ele normal, momento fletor ou cortante.
Tendo o diagrama da estrutura com cargas simétricas e anti-simetricas, basta somarmos os dois casos para obtermos o diagrama final, sendo assim teremos por exemplo:
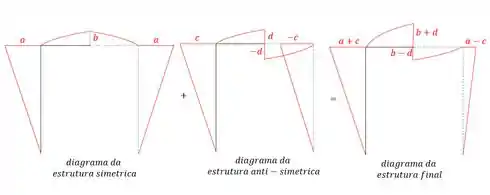
E lembre-se que isso valerá para tudo, tanto para reações de apoio, quanto para cortantes, momentos, normais e outros esforços.
Ufa, agora que terminamos vamos treinar para ficarmos craques nesses exercícios.