Rigidez Relativa
Produzido por Pablo RicardoTeoria
Introdução
No tópico anterior, aprendemos de maneira geral como resolver uma estrutura pelo método dos deslocamentos.
Nessa aula vamos começar a detalhar alguns macetes que vão nos ajudar a resolver os nossos problemas mais rápidos e mais precisamente.
Nesse primeiro caso com estruturas apenas com deslocabilidades internas, vamos ver um exemplo em que a ideia é aprendermos a usar o método de maneira rápida, e também aprender a simplificar a facilitar as nossas contas. Dito isso, bora partir pro nosso exemplo para pegarmos os macetes.
Rigidez relativa
Antes de irmos para o nosso exemplo, vale mostrar aqui um conceito bem legal de rigidez relativa, que vaia ajudar a gente nós nossos cálculos. Imagine que vc faz a conta e descobre as seguintes rigidezes:
seria muito complicado se tivéssemos por exemplo os seguintes valores:
Substituir esses valores seria muito ruim, então ao invés de usarmos as rigidezes aqui mostradas podemos simplificar elas, por exemplo, podemos dividir as rigidezes por:
Que fazendo essa conta teremos que:
Mas perceba que ainda temos uma inércia chatinha de calcular, as que podemos facilmente multiplicar por 10³, que no fim vai deixar de ser 0,024, e vai virar 24, que é mais fácil de calcular , e então teríamos as seguintes rigidezes:
Ou seja, bem mais fácil de usar. Mas temos algumas observações importantes:
- Aplicamos então o seguinte fator para as rigidezes relativas
- Esse fator ai em cima, terá que ser usado em todas as rigidezes, se usar só em um, vai dar errado, então tome muito cuidado de saber qual o fator usado para tornar a rigidez real em rigidez relativa.
- e
- e
- e
Que nada mais é que a junção dos dois facilitadores que usamos:
E agora a observação mais importante de todas, no final, quando determinarmos o valor de e eles vão estar calculados com os fatores
Ou seja, se quisermos saber a rotação real, precisaremos multiplicar o valor de e calculado pelo fator que usamos, que nesse caso é . Para não ficar tão abstrato, vamos fazer um exemplo completo para facilitar a visualização.
Exemplo
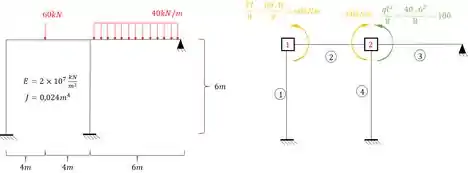
Como já sabemos, nesse tópico iremos usar apenas estruturas com deslocabilidades internas, e que já sabemos que o que devemos fazer para travar essas deslocabilidades internas é usar chapas. Sendo assim a nossa estrutura será:
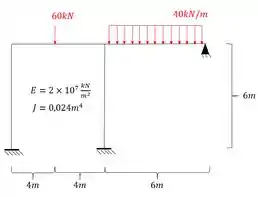
Como já sabemos, nossa estrutura apresenta apenas deslocabilidades internas, que são exatamente as deslocabilidades nos nós que não são nem apoio e nem rotulas, sendo assim teremos que a nossa estrutura travada com chapas será:
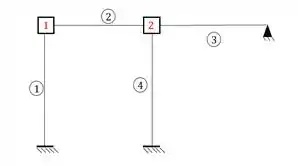
Sabemos que temos que determinar as nossas deformações: sendo assim sabemos que:
Perceba que a barra 2 possui chapas em ambas as extremidades, logo será biengastada, e como o carregamento nela é concentrado, usaremos a seguinte tabela:
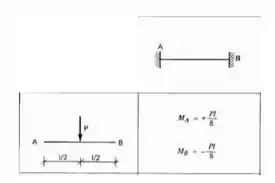
E para barra 3 ela possui um apoio de um lado e uma chapa de outro, logo será do tipo engastado apoiado, e a carga nele é distribuída, sendo assim nossa tabela será:
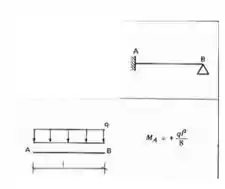
Calculando na nossa estrutura teremos que:
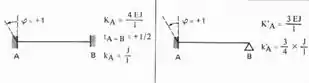
Sabemos aqui que temos que rotacionar a chapa 1, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 2 e 3 respeitando o caso biengastado ou engastado e apoiado:
E rotacionando a chapa 1 e aplicando as equações teremos:
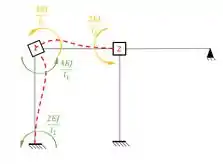
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Como já vimos no início dessa aula para este caso: . Substituindo teremos que:
Veja também que:
Como já usamos o fator de rigidez relativa, devemos continuar usando ele, e perceba que não podemos mudar mais, se usamos em um, temos que usar o mesmo em todos, sendo assim teremos que:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Sabemos aqui que temos que rotacionar agora a chapa 2, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 2 e 3 respeitando o caso biengastado ou engastado e apoiado:
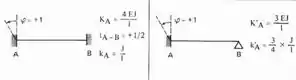
E rotacionando a chapa 2 e aplicando as equações teremos:
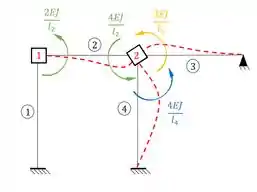
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Veja também que:
Como já usamos o fator de rigidez relativa, devemos continuar usando ele, e perceba que não podemos mudar mais, se usamos em um, temos que usar o mesmo em todos, sendo assim teremos que:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Sistema de equações
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Substituindo
Resolvendo esse sistema teremos que:
E se perguntarem quanto vale o momento na barra 2, no ponto que colocamos a chapa 1?
Ai primeiro precisamos dos momentos que agem na barra 2 e na chapa 1 nos sistemas 0, 1 e 2, sendo assim teremos que:
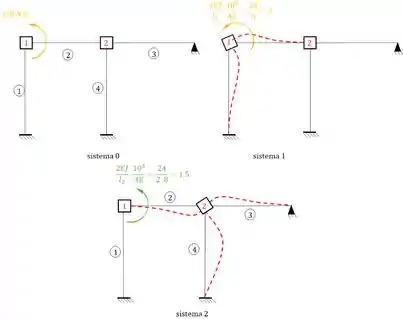
E usando a nossa fórmula teremos que:
E se pedissem as rotações nos pontos 1 e 2? Seria só colocar os valores de e , certo?
De certa forma isso é certo, mas não se esqueça que usamos uma rigidez relativa, ou seja, os e calculados levam em si essa relatividade, e a melhor forma de apagar isso é multiplicar os valores pelo coeficiente usado, sendo assim teremos que fazer:
Sendo assim se substituirmos teremos que:
E assim conseguimos entender como em sistemas apenas com deslocabilidades internas conseguimos determinar os deslocamentos, resolver o sistema de equações, determinar os momentos fletores por nó e por barra, e em fim determinamos os deslocamentos.
Agora bora treinar mais com mais exercícios, bora lá?