Apoios elásticos – Caso com Engastamento elástico
Produzido por Pablo RicardoTeoria
Como lidar com o nosso engaste elástico?
Antes de fazer um exemplinho pra facilitar o entendimento, temos que pegar o macete do que devemos fazer com a nossa mola. E para isso precisamos saber que existe um tratamento a ser feito no caso do sistema 0 (com carregamento externo) e um tratamento para os casos com rotação unitária dos nossos outros sistemas (1, 2, 3 ...), então vamos analisar essa diferença:
- Sistema 0
- Sistemas 1, 2, 3 ...
- Perceba que para as barras 1, possui chapa de ambos os lados, logo será considerada uma estrutura biengastada , e a carga nela é distribuída, sendo assim nossa tabela será:
- Já para a barra 2, ela possui um apoio de um lado (no ponto C) e uma chapa de outro (no ponto B), logo será do tipo engastado apoiado, e a carga nela é distribuída, sendo assim nossa tabela será:
No sistema 0 é bem tranquilinho, basta você substituir o engaste elástico por uma chapa, independente da posição que ele esteja, basta trocar a mola inteira por uma chapa e resolver como se fosse um nó com chapa como já conhecemos, então até aqui é bem de boas.
Nesse caso podemos lembrar os nossos conceitos de física, porque pensa só, colocamos uma chapa no lugar o engaste elástico, certo? Se rotacionarmos a chapa é como se rotacionássemos a mola, certo? Se isso acontece, como podemos determinar o momento fletor que vai agir na mola a partir de uma rotação imposta? Ai precisamos lembrar da nossa formulazinha:
Em que:
Entendido isso, bora partir para o nosso exemplinho que facilita bem esse entendimento.
Exemplo
Imagine que tenhamos que determinar a rotação na nossa mola da seguinte viga:
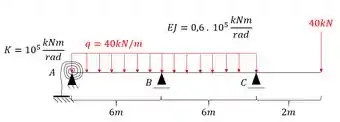
De inicio pode parecer complicado, mas vamos ver que é bem tranquilo de ser feito, então vamos lá.
Passo 1 – simplificação da estrutura
Veja que temos uma região em balanço, certo? Como já vimos em um exercício na aula sobre estruturas apenas com deslocabilidade interna, podemos trocar esse balanço por um momento que represente o que ele faz no ponto C, ou seja, como a carga de 40 kN traciona as fibras da parte de cima do ponto C, iremos por ali um momento que também tracione as fibras da parte de cima, dessa maneira iremos ter que:
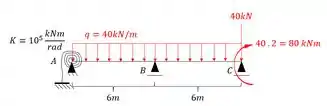
Passo 2 – determinação das deslocabilidades internas e suas chapas
A segunda coisa que precisamos lembrar é que precisamos por no apoio central uma chapa, certo? E com isso teríamos que:
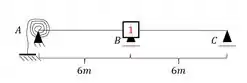
Sabemos que no apoio C não teremos chapa certo? Exatamente por ser um apoio extremo.
Mas no apoio A, como vimos no início dessa aula, se temos uma mola do tipo engaste elástico, obrigatoriamente trocamos ela por uma chapa, e então o nosso sistema a ser resolvido passa a ser:
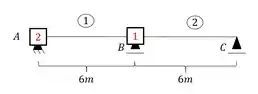
show? Bora pro próximo passo.
Passo 3 – solução do sistema 0
Vimos também no início dessa aula que para o sistema zero solucionamos o nosso problema como se não existisse a mola, ou seja, basta determinarmos os valores de e . Para isso temos:
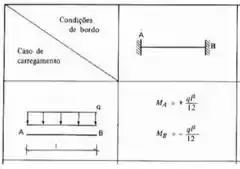
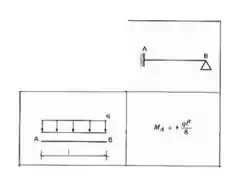
A única coisa que devemos tomar cuidado é de lembrar que como temo um mento fletor agindo no ponto C ele automaticamente se transforma em um engaste, e sabemos que barras bi-engastadas transferem metade do seu momento e conservam o sinal, sendo assim, se temos um momento de 80 kNm agindo em C, ela vai transferir pra B metade e com o mesmo sinal, ou seja, em modulo será 40 kNm.
Essa é a única parada que devemos tomar cuidado, iremos representar isso no desenho ali embaixo, mas achei que seria bom deixar bem explicadinho aqui em cima o motivo do que vai acontecer ali em baixo, exatamente pra não deixar dúvidas, beleza? Então vamos lá.
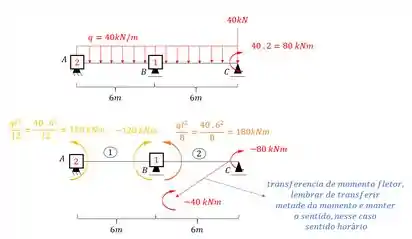
Com isso teremos que:
Passo 4 – solução do sistema 1
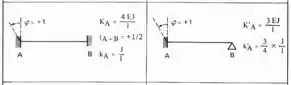
Sabemos que para solucionarmos o sistema 1, basta que rotacionemos a chapa 1, e com isso teremos como determinar o . Lembrando que sempre rotacionamos a nossa chapa no sentido anti-horário para mantermos o sinal positivo e sendo assim teremos a seguinte tabela a ser usada para as barras 1 e 2 respeitando o caso engastado e apoiado e o caso Bi-engastado:
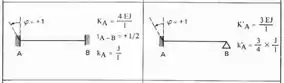
E rotacionando a chapa 1 e aplicando as equações teremos:
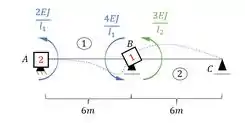
Veja que temos:
E:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Passo 5 – solução do sistema 2
Sabemos que para solucionarmos o sistema 2, basta que rotacionemos a chapa 1, e com isso teremos como determinar o . Lembrando que sempre rotacionamos a nossa chapa no sentido anti-horário para mantermos o sinal positivo e sendo assim teremos a seguinte tabela a ser usada para as barras 1 e 2 respeitando o caso engastado e apoiado e o caso Bi-engastado:
E rotacionando a chapa 2 e aplicando as equações teremos:
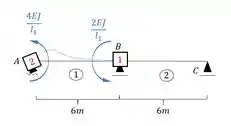
Veja que temos:
E:
Maaaaaaaaaaaaaas é aqui que devemos tomar o nosso cuidado. Lembra que a chapa 2 é uma mola? E que rotacionamos essa mola em 1 radiano? Ou seja, temos que somar esse momento gerado ao fator .
Como sabemos, a fórmula a ser usada é:
Somando teremos que:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Passo 6 – solução do sistema total
Substituindo:
Assim teremos que:
Lembre-se que o objetivo era a deformação na mola, certo? Ou seja, precisamos de , mas precisamos multiplicar ele pelo nosso fator de rigidez:
Ufa, enfim terminamos, agora bora fazer exercício pra ficar craque !!!!