Rigidez de um nó de uma viga
Produzido por Pablo RicardoTeoria
Introdução
No método das forças aprendemos que: Poderíamos usar uma carga unitária no ponto que queremos saber o deslocamento, no sentido e na direção do deslocamento que gostaríamos de conhecer, e essa carga unitária nos permitia determinar as deformações que chamávamos de deformações virtuais.
No método dos deslocamentos vamos usar um principio muito parecido. No caso do método dos deslocamentos ao invés de usarmos cargas unitárias para determinação de deformações, nós vamos usar deformações unitárias para determinação de cargas. Essas cargas que iremos encontrar são prioritariamente de momentos fletores, e esses momentos fletores são o que chamamos de Rigidez da nossa barra. Então em resumo podemos dizer que:
- A rigidez de uma barra é o momento fletor necessário para fazer essa barra rotacionar 1rad ou se deslocar uma distância .
- Vale lembrar que as rotações para nós serão ligadas as deslocabilidades internas, e os deslocamentos serão ligados as deslocabilidades externas.
Vamos analisar os principais casos para ficarmos tranquilos.
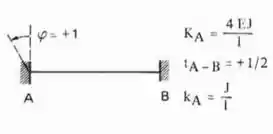
Mas antes vale lembrar que para nós o sinal dos momentos fletores serão considerados positivos sempre que estiverem no sentido anti-horário, como podemos ver aqui em baixo:
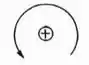
Obs: Todas as rigidezes aqui calculadas são para barras que possuem inércia constante, não se aplicando a barras com inércia variável.
Rotação de um dos apoio de uma viga Biengastada
Imagine que temos a seguinte viga de comprimento L:
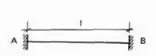
E decidimos rotacionar o apoio A dela em uma unidade de rotação, da seguinte maneira.

Essa rotação irá produzir os seguintes momentos fletores:
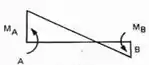
E usando as regrinhas de trabalho virtual, mas lembrando que dessa vez já temos as deformações e queremos determinar os momentos, obteremos os seguintes momentos fletores:
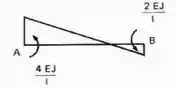
Ou seja, o momento fletor que aparece no apoio que foi rotacionado é de e o momento que essa rotação produz no outro apoio é dado por , que gira no mesmo sentido, e esses momentos são exatamente o que chamamos de rigidez dos nós A e B da nossa viga, que podemos chamar de , sendo assim teríamos as seguintes rigidezes da nossa viga biengastada.
- Nó A
- Nó B
- Nó A
- Nó B
- Nó A
- Nó B
- Nó A
- Nó B
Em alguns livros ainda podemos encontrar um tal de coeficiente de transmissão de uma viga (, que é basicamente a relação entre a rigidez do nó que subsequente ao que sofre a rotação e a rigidez do nó que de fato sofre a rotação, sendo assim teríamos que:
Rotação de um dos apoio de uma viga Engastada e apoiada
Imagine que temos a seguinte viga de comprimento L:
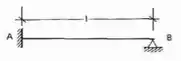
E decidimos rotacionar o apoio A dela em uma unidade de rotação, da seguinte maneira (e percebe que escolhemos o apoio A porque só podemos aplicar essa rotação nele, tendo em vista que o outro apoio é do segundo gênero e não possuirá momentos fletores).
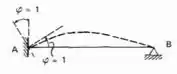
E usando as regrinhas de trabalho virtual, mas lembrando que dessa vez já temos as deformações e queremos determinar os momentos, obteremos os seguintes momentos fletores:
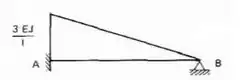
Ou seja, o momento fletor que aparece no apoio que foi rotacionado é de e o momento que essa rotação produz no outro apoio é dado por , e esses momentos são exatamente o que chamamos de rigidez dos nós A e B da nossa viga, que podemos chamar de , sendo assim teríamos as seguintes rigidezes da nossa viga engastada e apoiada.
Em alguns livros ainda podemos encontrar um tal de coeficiente de transmissão de uma viga (, que é basicamente a relação entre a rigidez do nó que subsequente ao que sofre a rotação e a rigidez do nó que de fato sofre a rotação, sendo assim teríamos que:
Deslocamento do apoio de um valor na viga Biengastada
Como vimos, as rotações estão ligadas as deslocabilidades internas, e com isso os deslocamentos estarão ligados as deslocabilidades externas, sendo assim teremos que:
Imagine que temos a seguinte viga de comprimento L:
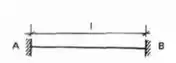
E decidimos deslocar o apoio B dela em um valor , da seguinte maneira.

Esse deslocamento irá produzir os seguintes momentos fletores:
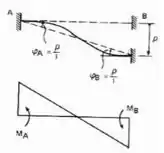
E usando as regrinhas de trabalho virtual, mas lembrando que dessa vez já temos as deformações e queremos determinar os momentos, obteremos os seguintes momentos fletores:
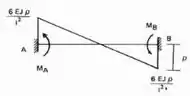
Ou seja, o momento fletor que aparece no apoio que foi deslocado é de e o momento que esse deslocamento produz no outro apoio é dado por , girando no mesmo sentido, e esses momentos são exatamente o que chamamos de rigidez dos nós A e B da nossa viga, que podemos chamar de , sendo assim teríamos as seguintes rigidezes da nossa viga engastada e apoiada.
Em alguns livros ainda podemos encontrar um tal de coeficiente de transmissão de uma viga (, que é basicamente a relação entre a rigidez do nó que subsequente ao que sofre a rotação e a rigidez do nó que de fato sofre a rotação, sendo assim teríamos que:
Deslocamento do apoio de um valor na viga Engastada e Apoiada
Imagine que temos a seguinte viga de comprimento L:

E decidimos deslocar o apoio B dela em um valor , da seguinte maneira.
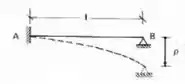
Esse deslocamento irá produzir os seguintes momentos fletores:
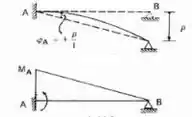
E usando as regrinhas de trabalho virtual, mas lembrando que dessa vez já temos as deformações e queremos determinar os momentos, obteremos os seguintes momentos fletores:

Ou seja, o momento fletor que aparece no apoio que foi deslocado é de e o momento que essa rotação produz no outro apoio é dado por , girando no sentido anti-horário, e esses momentos são exatamente o que chamamos de rigidez dos nós A e B da nossa viga, que podemos chamar de , sendo assim teríamos as seguintes rigidezes da nossa viga engastada e apoiada.
Em alguns livros ainda podemos encontrar um tal de coeficiente de transmissão de uma viga (, que é basicamente a relação entre a rigidez do nó que subsequente ao que sofre o deslocamento e a rigidez do nó que de fato sofre a deslocamento, sendo assim teríamos que:
Tabela simplificada
Ou seja, podemos juntar tudo que vimos aqui na seguinte tabela, e perceba que na nossa tabela ainda temos alguns outros casos que não apresentamos aqui em cima, mas que seguem exatamente o mesmo padrão:
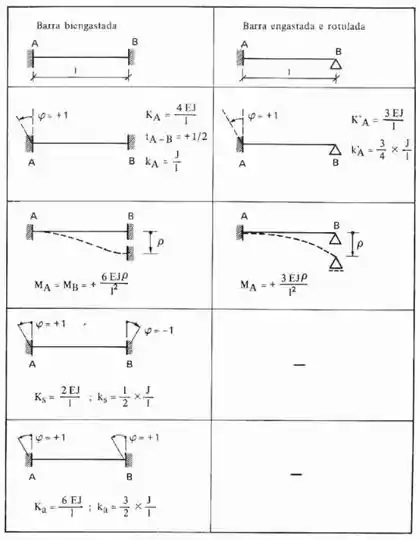
Entendido isso, bora fazer uns exercícios antes de partirmos para o passo a passo do nosso problema do método dos deslocamentos.
Vale lembrar que lá já vamos usar os conceitos de rigidez na pratica, por isso é bom entender bem cada fórmula, cada caso e também os sinais que estamos arbitrando, ou seja, positivo no sentido anti-horário.
Rotação de um dos apoio de uma viga Biengastada
Rotação de um dos apoio de uma viga Engastada e apoiada
Deslocamento do apoio de um valor ρ na viga Biengastada
Deslocamento do apoio de um valor ρ na viga Engastada e Apoiada
Tabela simplificada
Exercícios Resolvidos
Exercício Resolvido #1
José Carlos Sussekind, Curso de análise estrutural 3, 7ª ed. Rio de Janeiro: Globo, 1987, pp. 172. exercício 10.3 (Adaptado)
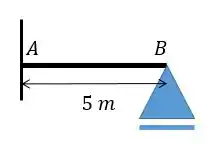
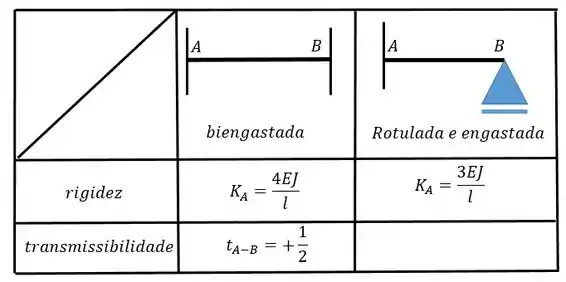
Com o auxílio da tabela calcule a rigidez e a rigidez específica da barra nos nós e . Sabendo que e .
Passo 1
Faaala, galerinha!!! Aqui temos um exercício com uma viga simples engastada no lado e apoiada no lado e queremos achar a rigidez e a rigidez específica . Lembrando que a relação entre as duas é:
Outra coisa que a gente deve lembrar é que tanto o apoio de primeiro quanto segundo gênero estão suscetíveis à rotação, dessa forma pode-se falar que o lado apoiado está rotulado.
Agora é olhar para a tabela e resolver o probleminha que é bem direto. Vamos fazer isso juntos nos próximos passos =D
Passo 2
Quando a gente olha o nosso problema e a nossa tabela a gente percebe que só existe uma possibilidade de rigidez para o nó (não é mesmo? A barra está engastada e apoiada) então vamos ter:
Agora é só substituir os valores:
Mas podemos escrever com uma forma mais usual:
Que belezaaa.
Passo 3
Agora podemos calcular a rigidez específica da barra em .
Substituindo:
Passo 4
Para a barra nós vamos ter que a rigidez é nula. Isso acontece porque o nó não resiste à rotação. Então:
Por isso que a tabela não fornece o valor do coeficiente de transmissibilidade para o nó , porque na real esse coeficiente é igual a zero!
Resposta
Exercício Resolvido #2
Origem do Exercício
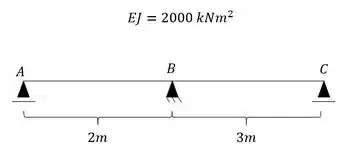
para a viga abaixo represente cada trecho de viga como uma viga separada e determine as rigidezes que podem aparecer para cada um dos trechos analisados.
Passo 1
Como vimos na teoria, o que está ligado a cada uma das deslocabilidades segue o seguinte padrão:
- Para deslocabilidades internas usamos as rigidezes voltadas para rotação
- Para deslocabilidade externas usamos as rigidezes voltadas para deslocamento
Sendo assim teremos que determinar primeiro o tipo de deslocabilidades que temos na nossa viga.
Passo 2
Vamos analisar primeiro as deslocabilidades ligadas a cada um dos apoios:
- Apoio A e C
- Apoio B
- Total de deslocabilidades
- Temos uma viga do tipo engastada e apoiada
- O tipo de deslocabilidade dela é interna (ou seja, ligada a rotação)
Perceba que ele não pode se deslocar na vertical, nem na horizontal, mas pode rotacionar, logo, não temos deslocabilidades externas, porém tome cuidado, perceba que nesse ponto temos uma extremidade de viga, ou seja, não temos momento, e ela funciona como rotula, dessa maneira, como funciona como rotula, não precisamos contabilizar.
O apoio B possue deslocabilidade internas, porque pode rotacionar, porém, não possui deslocabilidade externas, e dessa maneira concluímos que a nossa viga só possui deslocabilidade do tipo interna.
Passo 3
Tendo isso precisamos agora separar a nossa viga, quebrando a deslocabilidade existente:
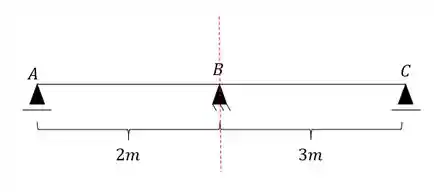
Perceba que se rompêssemos a nossa viga no apoio B, teríamos valores de reação vertical, horizontal e de momentos fletores, ou seja, nosso apoio B seria a representação de um engaste, que poderíamos agrupar como:
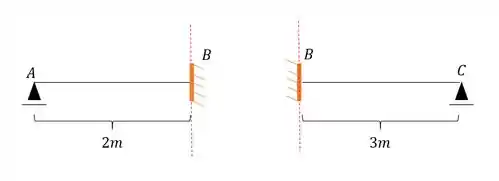
Passo 4
Agora já fizemos o mais difícil, quando chegarmos na aula do passo a passo de método das deslocabilidades vamos ver que não há necessidade de ficarmos dividindo toda a nossa estrutura, mas estamos fazendo isso aqui para deixar bem claro o porque de usarmos certas fórmulas ao invés de outras, então pode estar dando um trabalhinho agora, mas depois vai ficar mais tranquilo:
Sendo assim, olhando o nosso desenho, só precisamos determinar a nossa fórmula, com isso basta listarmos o que temos, que é:
Logo a fórmula que devemos usar é essa aqui
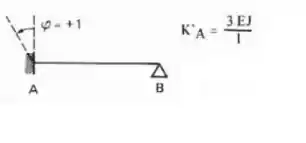
Aplicando a nossa viga, a cada uma de cada vez teremos:
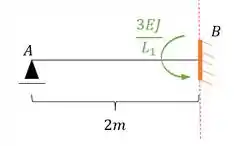
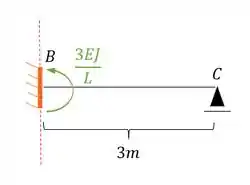
- Metade mais a esquerda
- Metade mais a direita
Vamos gira-la sempre no sentido anti-horário para podermos ter as rigidezes sempre positivas, sendo assim teremos que:
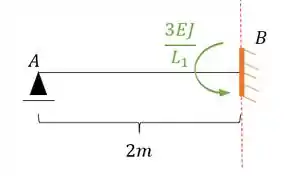
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
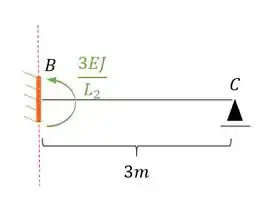
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Resposta
Exercício Resolvido #3
Origem do Exercício
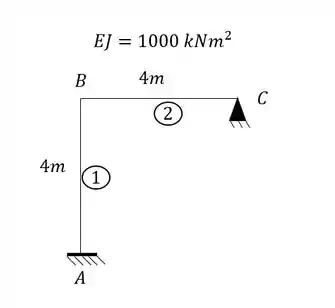
para o pórtico abaixo represente cada trecho como uma viga separada e determine as rigidezes que podem aparecer para cada um dos trechos analisados.
Passo 1
Como vimos na teoria, o que está ligado a cada uma das deslocabilidades segue o seguinte padrão:
- Para deslocabilidades internas usamos as rigidezes voltadas para rotação
- Para deslocabilidade externas usamos as rigidezes voltadas para deslocamento
Sendo assim teremos que determinar primeiro o tipo de deslocabilidades que temos na nossa viga.
Passo 2
Vamos analisar primeiro as deslocabilidades ligadas a cada um dos apoios:
- Apoio A e C
- Apoio B
- Total de deslocabilidades
- Temos uma viga do tipo engastada e apoiada
- O tipo de deslocabilidade dela é interna (ou seja, ligada a rotação)
- Trecho horizontal
- Perceba que temos uma viga do tipo Bi-engastada
- Os tipos de deslocabilidades dela são internas (ou seja, ligada a rotação)
- Trecho vertical
Os apoios A e C são apoio do tipo engaste, logo não possuem nem deslocabilidade interna e nem deslocabilidade externa.
O apoio B está ligado aos engastes da base, que são indeslocaveis, logo o nó B não possui deslocabilidade externa, porém veja que ele pode rotacionar, dessa forma, identificamos que o nó possui deslocabilidade interna, sendo nesse caso, contabilizado, uma deslocabilidade interna.
Passo 3
Tendo isso precisamos agora separar o nosso pórtico, e para isso quebramos apenas a deslocabilidade interna que foi contabilizada:
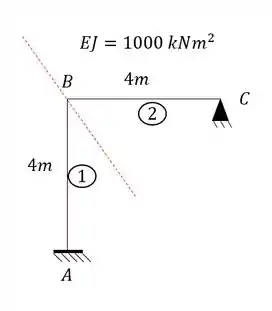
Perceba que se rompêssemos o nosso pórtico no apoio B, teríamos valores de reação vertical, horizontal e de momentos fletores, ou seja, nosso nó B seria a representação de um engaste, que poderíamos agrupar como:
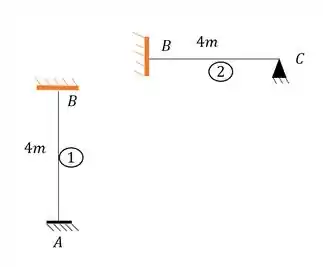
Passo 4
Agora já fizemos o mais difícil, quando chegarmos na aula do passo a passo de método das deslocabilidades vamos ver que não há necessidade de ficarmos dividindo toda a nossa estrutura, mas estamos fazendo isso aqui para deixar bem claro o porque de usarmos certas fórmulas ao invés de outras, então pode estar dando um trabalhinho agora, mas depois vai ficar mais tranquilo:
Sendo assim, olhando o nosso desenho, só precisamos determinar a nossa fórmula, com isso basta listarmos o que temos, que é:
Logo a fórmula que devemos usar é essa aqui
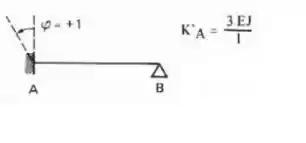
Aplicando a nossa viga teremos que:
Vamos gira-la sempre no sentido anti-horário para podermos ter as rigidezes sempre positivas, sendo assim teremos que:
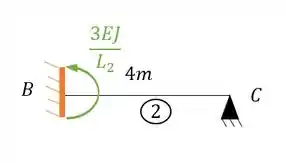
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Logo a fórmula que devemos usar é essa aqui
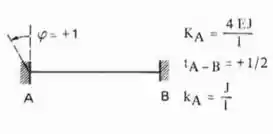
Aplicando a nossa viga, teremos:
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva mesmo, sendo assim teremos que:
Perceba que temos também o ponto A, logo:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Resposta
Exercício Resolvido #4
José Carlos Sussekind, Curso de análise estrutural 3, 7ª ed. Rio de Janeiro: Globo, 1987, pp. 172. exercício 10.9 (Adaptado)
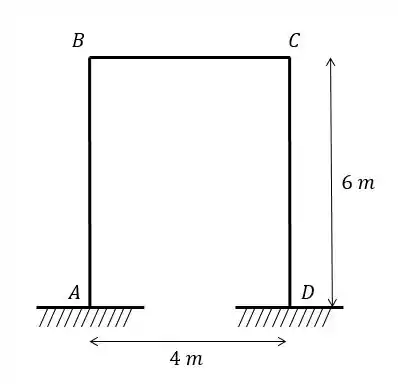
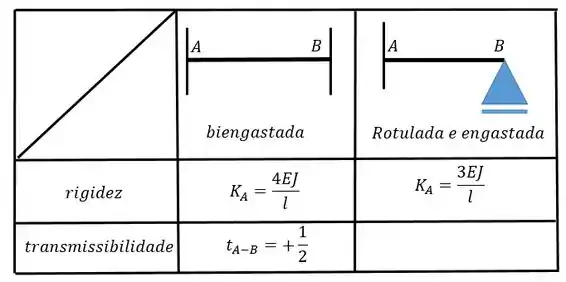
Com o auxílio da tabela calcule a rigidez e a rigidez específica do nó . Sabendo que e .
Passo 1
Faaala, galerinha!!! Aqui temos um exercício com um pórtico engastado nas bases e queremos achar a rigidez e a rigidez específica do nó . Lembrando que a relação entre as duas é:
Para resolver esse exercício vamos olhar na tabela e descobrir qual melhor equação utilizar, mas para isso nós precisamos dividir as barras corretamente. O que consiste em saber onde estão os pontos sujeitos à rotação.
Passo 2
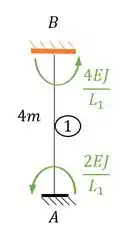
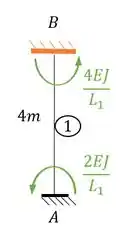
Os nós que estão sujeitos à rotação são os nós e , logo esses nós são separados da nossa estrutura e substituídos por engastes:
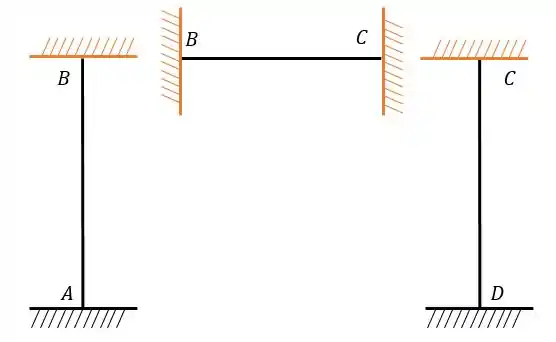
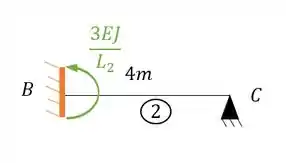
Perceba que a gente vai tratar o nosso pórtico como três barras distintas, como queremos apenas as grandezas referentes ao nó vamos olhar para as barras e . Ambas são biengastadas, logo nossa equação será:
Fazendo para a barra vamos ter:
Mas podemos escrever com uma forma mais usual:
E para a barra vamos ter:
Mas podemos escrever com uma forma mais usual:
Passo 3
Agora podemos calcular a rigidez específica. Para a barra :
Substituindo:
Para a barra :
Substituindo:
Resposta
Para a barra :
Para a barra :
Exercício Resolvido #5
José Carlos Sussekind, Curso de análise estrutural 3, 7ª ed. Rio de Janeiro: Globo, 1987, pp. 172. exercício 10.9 (Adaptado)
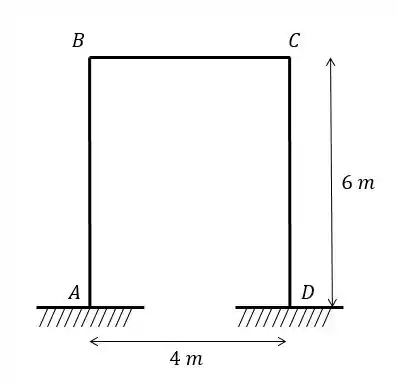
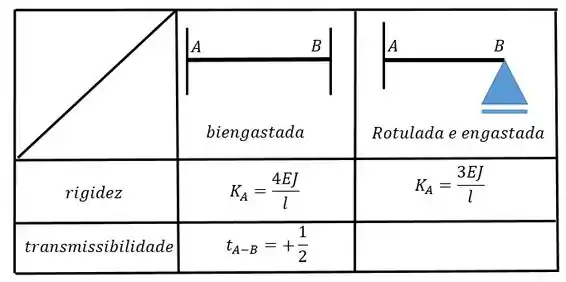
Sabendo que o nó , quando analisado segundo a barra , do pórtico abaixo possui rigidez absoluta Calcule a rigidez do nó .
Passo 1
Pessoal, essa questão aqui já nos fornece a rigidez do nó e pede a rigidez do nó . Como esses dois nós estão interligados por meio de uma barra, então a gente pode aplicar o conceito de transmissibilidade.
Passo 2
Para resolver isso então é só aplicar o coeficiente de transmissibilidade . A gente só tem que ficar esperto porque na tabela e são genéricos então podem não representar exatamente os nós e do problema, beleza? No nosso problema nos foi dado o , e isso corresponde ao da tabela, ok? É só ver aonde que foi feita a separação. Como na figura abaixo:
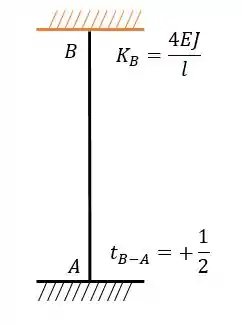
Perceba que os nós e estão trocados, então vamos ter que:
É assim que funciona o coeficiente de transmissibilidade!
Resposta
Exercício Resolvido #6
Origem do Exercício
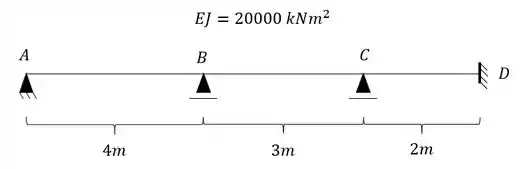
para a viga abaixo represente cada trecho de viga como uma viga separada e determine as rigidezes que podem aparecer para cada um dos trechos analisados.
Passo 1
Como vimos na teoria, o que está ligado a cada uma das deslocabilidades segue o seguinte padrão:
- Para deslocabilidades internas usamos as rigidezes voltadas para rotação
- Para deslocabilidade externas usamos as rigidezes voltadas para deslocamento
Sendo assim teremos que determinar primeiro o tipo de deslocabilidades que temos na nossa viga.
Passo 2
Vamos analisar primeiro as deslocabilidades ligadas a cada um dos apoios:
- Apoio A
- Apoio B e C
- Apoio D
- Total de deslocabilidades
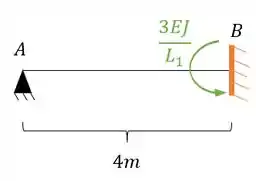
- Temos uma viga do tipo engastada e apoiada
- O tipo de deslocabilidade dela é interna (ou seja, ligada a rotação)
- Metade mais a esquerda
- Perceba que temos duas vigas do tipo Bi-engastada
- Os tipos de deslocabilidades dela são internas (ou seja, ligada a rotação)
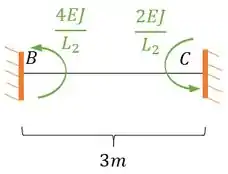
- Trecho central
- Metade mais a direita
Perceba que ele não pode se deslocar na vertical, nem na horizontal, mas pode rotacionar, logo, não temos deslocabilidades externas, porém tome cuidado, perceba que nesse ponto temos uma extremidade de viga, ou seja, não temos momento, e ela funciona como rotula, dessa maneira, como funciona como rotula, não precisamos contabilizar.
Os apoios B e C possuem deslocabilidades internas também, porque ambos podem rotacionar, porém, não possuíram deslocabilidade externas. Assim contabilizamos 2 deslocabilidades.
O apoio D não possui deslocabilidade interna por ser um engaste, e também não possui deslocabilidades externas.
Passo 3
Tendo isso precisamos agora separar a nossa viga, e para isso quebramos apenas as deslocabilidades internas que foram contabilizadas:
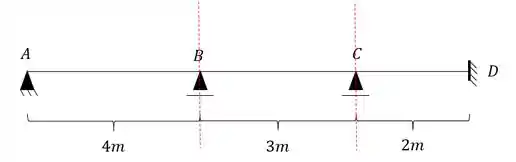
Perceba que se rompêssemos a nossa viga no apoio B e C, teríamos valores de reação vertical, horizontal e de momentos fletores, ou seja, nosso apoio B e C seriam a representação de um engaste, que poderíamos agrupar como:
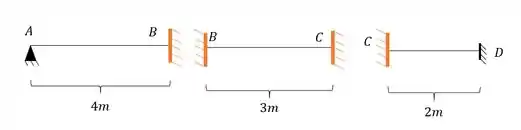
Passo 4
Agora já fizemos o mais difícil, quando chegarmos na aula do passo a passo de método das deslocabilidades vamos ver que não há necessidade de ficarmos dividindo toda a nossa estrutura, mas estamos fazendo isso aqui para deixar bem claro o porque de usarmos certas fórmulas ao invés de outras, então pode estar dando um trabalhinho agora, mas depois vai ficar mais tranquilo:
Sendo assim, olhando o nosso desenho, só precisamos determinar a nossa fórmula, com isso basta listarmos o que temos, que é:
Logo a fórmula que devemos usar é essa aqui
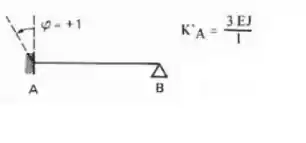
Aplicando a nossa viga, teremos:
vamos sempre rotacionar no sentido anti-horário para podermos manter as rigidezes sempre positivas.
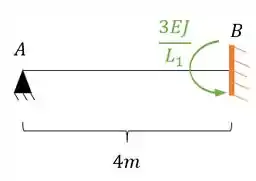
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Logo a fórmula que devemos usar é essa aqui
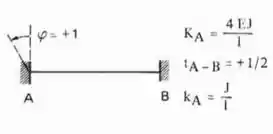
Aplicando a nossa viga, teremos:
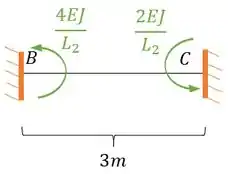
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva mesmo, sendo assim teremos que:
Perceba que temos também o ponto C, logo:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
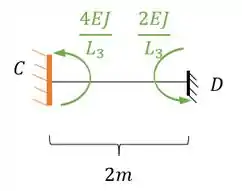
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
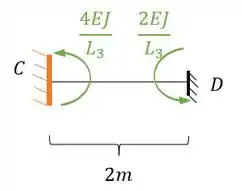
Perceba que temos também o ponto D, logo:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Resposta
Exercício Resolvido #7
Origem do Exercício
para o pórtico abaixo represente cada trecho como uma viga separada e determine as rigidezes que podem aparecer para cada um dos trechos analisados.
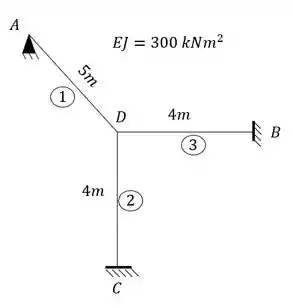
Passo 1
Como vimos na teoria, o que está ligado a cada uma das deslocabilidades segue o seguinte padrão:
- Para deslocabilidades internas usamos as rigidezes voltadas para rotação
- Para deslocabilidade externas usamos as rigidezes voltadas para deslocamento
Sendo assim teremos que determinar primeiro o tipo de deslocabilidades que temos na nossa viga.
Passo 2
Vamos analisar primeiro as deslocabilidades ligadas a cada um dos apoios:
- Apoio A
- Apoio D
- Apoios B e C
- Total de deslocabilidades
- Temos uma viga do tipo engastada e apoiada (viga 1)
- O tipo de deslocabilidade dela é interna (ou seja, ligada a rotação)
- Trecho superior
- Perceba que temos duas vigas do tipo Bi-engastada (viga 2 e 3)
- Os tipos de deslocabilidades dela são internas (ou seja, ligada a rotação)
- Trecho direito
- Metade mais inferior
Perceba que ele não pode se deslocar na vertical, nem na horizontal, mas pode rotacionar, logo, não temos deslocabilidades externas, porém tome cuidado, perceba que nesse ponto temos uma extremidade de viga, ou seja, não temos momento, e ela funciona como rotula, dessa maneira, como funciona como rotula, não precisamos contabilizar.
O apoio D possui deslocabilidade interna também, porque pode rotacionar, porém, não possui deslocabilidade externas. Assim contabilizamos 1 deslocabilidade.
Os apoios B e C não possui deslocabilidade interna por serem um engaste, e também não possui deslocabilidades externas.
Passo 3
Tendo isso precisamos agora separar o nosso pórtico, e para isso quebramos apenas as deslocabilidades internas que foram contabilizadas:
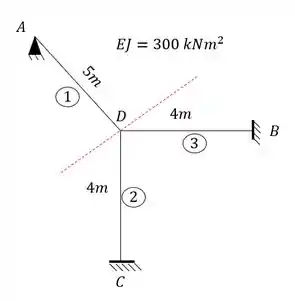
Perceba que se rompêssemos o nossos pórtico no apoio D, teríamos valores de reação vertical, horizontal e de momentos fletores, ou seja, nosso apoio D seria a representação de um engaste, que poderíamos agrupar como:
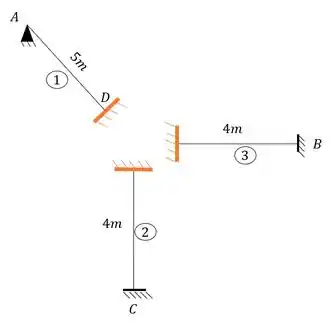
Passo 4
Agora já fizemos o mais difícil, quando chegarmos na aula do passo a passo de método das deslocabilidades vamos ver que não há necessidade de ficarmos dividindo toda a nossa estrutura, mas estamos fazendo isso aqui para deixar bem claro o porque de usarmos certas fórmulas ao invés de outras, então pode estar dando um trabalhinho agora, mas depois vai ficar mais tranquilo:
Sendo assim, olhando o nosso desenho, só precisamos determinar a nossa fórmula, com isso basta listarmos o que temos, que é:
Logo a fórmula que devemos usar é essa aqui
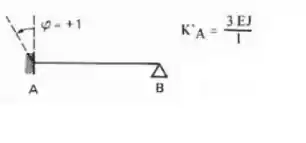
Aplicando a nossa viga, teremos:
Vamos rotacionar no sentido anti-horário para sempre podermos manter os sinais positivos, sendo assim teremos:
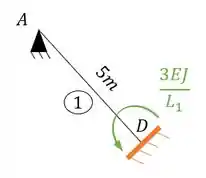
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Logo a fórmula que devemos usar é essa aqui
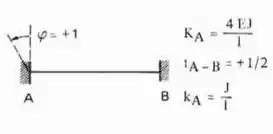
Aplicando a nossa viga, teremos:
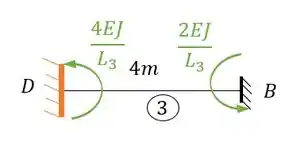
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva mesmo, sendo assim teremos que:
Perceba que temos também o ponto B, logo:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
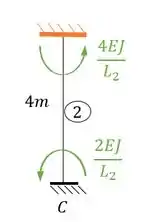
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Perceba que temos também o ponto C, logo:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário também, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Resposta
Exercício Resolvido #8
Origem do Exercício
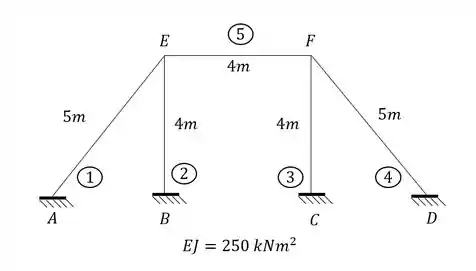
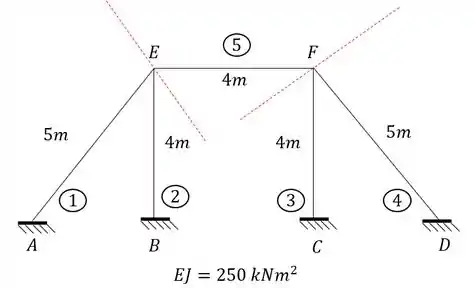
para o pórtico abaixo represente cada trecho como uma viga separada e determine as rigidezes que podem aparecer para cada um dos trechos analisados.
Passo 1
Como vimos na teoria, o que está ligado a cada uma das deslocabilidades segue o seguinte padrão:
- Para deslocabilidades internas usamos as rigidezes voltadas para rotação
- Para deslocabilidade externas usamos as rigidezes voltadas para deslocamento
Sendo assim teremos que determinar primeiro o tipo de deslocabilidades que temos na nossa viga.
Passo 2
Vamos analisar primeiro as deslocabilidades ligadas a cada um dos apoios:
- Apoio A, B, C e D
- Apoios E e F
- Total de deslocabilidades
- Perceba que todas as nossas vigas são Bi-engastadas
- Os tipos de deslocabilidades dela são internas (ou seja, ligada a rotação)
Os apoios A, B, C e D são apoio do tipo engaste, logo não possuem nem deslocabilidade interna e nem deslocabilidade externa.
Os apoios E e F estão ligados aos engastes das bases, que são indeslocaveis, logo os nós E e F não possuem deslocbilidade externa, porém veja que eles podem rotacionar, dessa forma, identificamos que os nós possuem deslocabilidade interna, sendo nesse caso, contabilizado, duas deslocabilidades internas.
Passo 3
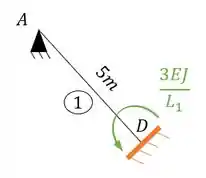
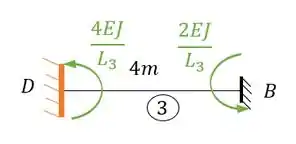
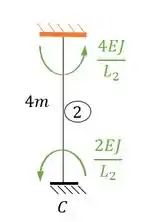
Tendo isso precisamos agora separar o nosso pórtico, e para isso quebramos apenas as deslocabilidades internas que foram contabilizadas:
Perceba que se rompêssemos o nosso pórtico no apoio E e F, teríamos valores de reação vertical, horizontal e de momentos fletores, ou seja, nossos apoios em E e F seria a representação de um engaste, que poderíamos agrupar como:
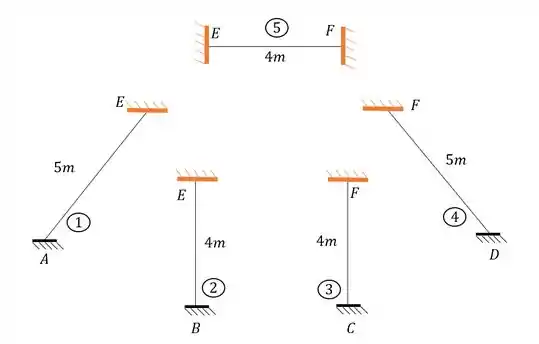
Passo 4
Agora já fizemos o mais difícil, quando chegarmos na aula do passo a passo de método das deslocabilidades vamos ver que não há necessidade de ficarmos dividindo toda a nossa estrutura, mas estamos fazendo isso aqui para deixar bem claro o porque de usarmos certas fórmulas ao invés de outras, então pode estar dando um trabalhinho agora, mas depois vai ficar mais tranquilo:
Sendo assim, olhando o nosso desenho, só precisamos determinar a nossa fórmula, com isso basta listarmos o que temos, que é:
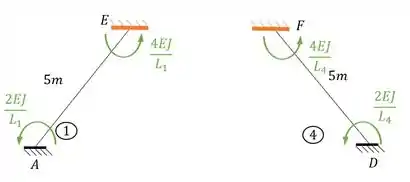
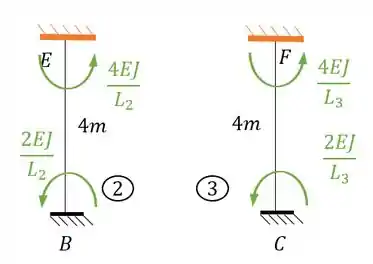
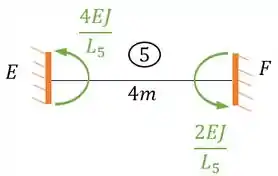
Logo a fórmula que devemos usar é essa aqui
Aplicando a nossa viga, teremos:
- Barra 1 e 4
- Barra 2 e 3
- Barra 5
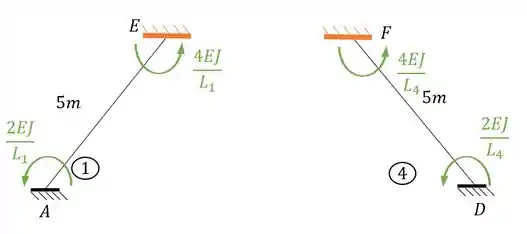
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva mesmo, sendo assim teremos que:
Calculando o outro ponto temos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
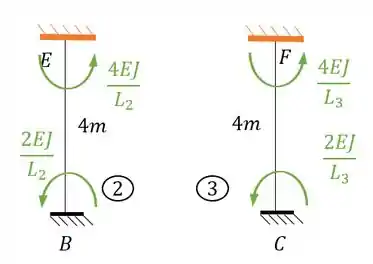
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Calculando o outro ponto temos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário também, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
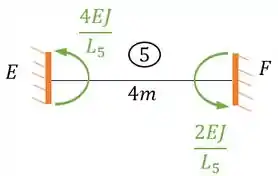
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Calculando o outro ponto temos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário também, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Resposta